Graphe de Gran
Un graphe de Gran est un moyen courant d'étalonner un titrate ou un titrant en estimant le volume d'équivalence pendant une titrage d'un acide fort avec une base forte ou pendant un titrage potentiométrique.
Recherche sur Google Images :

Source image : fr.wikipedia.org Cette image est un résultat de recherche de Google Image. Elle est peut-être réduite par rapport à l'originale et/ou protégée par des droits d'auteur. |
Page(s) en rapport avec ce sujet :
- Allure du graphe pH = f (v). - Détermination du point équivalent : * Méthode des deux tangentes. * Méthode de Gran. 3. Dosage d'un acide faible par une base... (source : cpge.lycee-marceau)
- Titrage de la glycine. Introduction. La glycine est un acide a-aminé..... volume équivalent peut-on déterminer expérimentalement par la méthode de Gran ?... Auquel des deux p de la glycine peut-on accéder par lecture graphique simple... (source : s2.e-monsite)
Un graphe de Gran (aussi méthode de Gran et titrage de Gran) est un moyen courant d'étalonner un titrate ou un titrant en estimant le volume d'équivalence pendant une titrage d'un acide fort avec une base forte ou pendant un titrage potentiométrique. De tels graphes peuvent aussi servir à estimer le contenu en carbonate d'une solution aqueuse, mais aussi les constantes d'acidité Ka d'acides ou bases faibles à partir de données de titrage.
Les graphes de Gran mettent en œuvre des approximations linéaires de relations a priori non-linéaires entre la quantité mesurée, le pH ou le potentiel électromoteur (f. e. m. ), et le volume de titrant ajouté. D'autres types de mesures de concentration, tels que l'absorbance spectrophotométrique ou les déplacements chimiques en RMN, peuvent habituellement aussi servir. Ces approximations ne sont valides que près du point d'équivalence, mais non pas au point d'équivalence, et par conséquent la méthode diffère des autres estimations de point d'équivalence utilisant les premiers ou seconds dérivés, méthodes qui requièrent des données au point d'équivalence. A l'origine, c'est-à-dire avant l'arrivée d'ordinateurs, les graphes de Gran ont été conçus comme détermination graphique, où un tracé sur papier quadrillé serait manuellement extrapolé pour estimer l'intercepte sur l'abscisse (l'axe du volume). Ce procédé a été depuis remplacé par l'analyse plus précise par la méthode des moindres carrés, en particulier avec logiciels de feuilles de calcul qui possèdent une fonction intégrée appliquant la méthode des moindres carrées.
Titrage d'acide fort par base forte
Lors d'un titrage pH-métrique d'une solution d'acide fort, nous avons à chaque ième point,
où Kw est la constante de autoprotolyse de l'eau.
Si le volume de départ de l'acide est 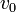 et sa concentration
et sa concentration ![[Hˆ+]_{0ˆ{ }}](illustrations/8144701b6d4768b0f84f6395ac6373c6.png) , et si le titrage utilise une base de concentration
, et si le titrage utilise une base de concentration ![[OHˆ-]_{0ˆ{ }}](illustrations/a6768ed3c004ea99b7818ac314e0f47c.png) , à tout ième point au cours du titrage avec un volume cumulé de titrant
, à tout ième point au cours du titrage avec un volume cumulé de titrant 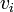 ,
,

Au point d'équivalence, le volume d'équivalence 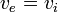 .
.
Or,
 un graphe de un graphe de |
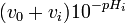 vs. vs. 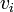 |
aura une région linéaire | avant | l'équivalence, avec pente | ![-[OHˆ-]_{0ˆ{ }}](illustrations/5f33e1b6659cb095ee8ace58c6600f52.png) |
 et un graphe de et un graphe de |
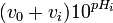 vs. vs. 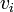 |
aura une région linéaire | après | l'équivalence, avec pente | ![[OHˆ-]_0/K_{wˆ{ }}](illustrations/95483d311f0fbfbdd34b5a244decd048.png) |
 les deux graphes auront les deux graphes auront |
![v_e=v_0 [Hˆ+]_0/[OHˆ-]_{0ˆ{ }}](illustrations/fa8f22bf3df8051351474ba8990a1d2d.png) |
comme intercepte de l'abscisse |
Le volume d'équivalence ve est utilisé pour calculer l'inconnu, soit ![[Hˆ+]_{0ˆ{ }}](illustrations/8144701b6d4768b0f84f6395ac6373c6.png) ou
ou ![[OHˆ-]_{0ˆ{ }}](illustrations/a6768ed3c004ea99b7818ac314e0f47c.png) .
.
Avant d'entamer le titrage, le pH-mètre est d'habitude calibré avec solutions tampons aux pH connus. La puissance ionique peut être maintenue par un choix judicieux de l'acide et de la base. A titre d'exemple, un titrage de l'acide HCl avec la base NaOH d'à-peu-près la même concentration remplacera H+ par un ion de même charge (Na+) à plus ou moins la même concentration, pour maintenir la puissance ionique assez constante. Autrement, on peut utiliser une concentration assez élevée d'électrolyte de fond, ou le cœfficient d'activité peut être calculé. [1]
Titrage de base forte par acide fort
Des graphes miroitant les précédents sont obtenus avec un titrage de base forte par acide fort, et les pentes sont renversées.
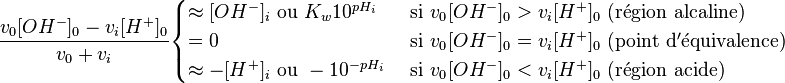
Donc,

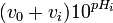 vs.
vs. 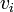 aura une région linéaire avant l'équivalence avec pente
aura une région linéaire avant l'équivalence avec pente ![-[Hˆ+]_0/K_{wˆ{ }}](illustrations/a4b3dbe3e9f4730ccb571e559010d239.png)
 et
et 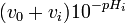 vs.
vs. 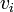 aura une région linéaire après l'équivalence avec pente
aura une région linéaire après l'équivalence avec pente ![[Hˆ+]_{0ˆ{ }}](illustrations/8144701b6d4768b0f84f6395ac6373c6.png)
 les deux graphes auront
les deux graphes auront ![v_e=v_0 [OHˆ-]_{0ˆ{ }}/[Hˆ+]_0](illustrations/233b891824c3aa2fbc69e919629eeb89.png) comme intercepte de l'abscisse
comme intercepte de l'abscisse
La Figure 1 présente des graphes de Gran suite à un titrage d'une base forte par un acide fort.
Concentrations et constantes de dissociation d'acides faibles
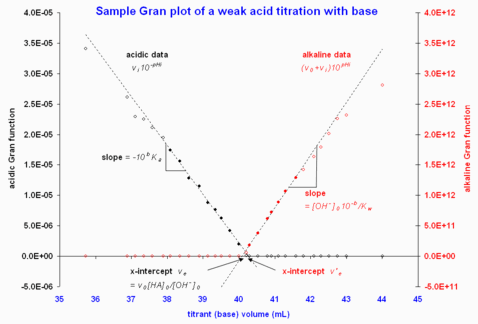
Figure 2. graphes de Gran illustratifs à partir des données d'une source en ligne. Consulté le 2008-02-18 Seule la région près de l'équivalence est présentée, puisque les données loin du point d'équivalence devient fortement de la linéarité. Les cercles emplis indiquent les points retenus pour le calcul de l'intercepte par la méthode des moindres carrées donnant les courbes pointillées.
La méthode peut estimer les constantes de dissociation d'acides faibles, mais aussi leurs concentrations (Gran, 1952). Si l'acide est representé par HA, où
![K_a = \frac{[Hˆ+]_i[Aˆ-]_i}{[HA]_i}](illustrations/ab98d889b8f6e03063ebfa77d7239869.png) ,
,
on aura à chaque ième point d'un titrage d'un volume v0 d'un acide à concentration [HA]0 par une base à concentration [OH − ]0 dans la région linéaire loin d'équivalence
![[HA]_i \approx \frac{v_0 [HA]_0-v_i[OHˆ-]_0}{v_0+v_i}](illustrations/12ad61b97d063e1f5f2ed55f1a8de914.png) and
and![[Aˆ-]_i \approx \frac{v_i[OHˆ-]_0}{v_0+v_i}](illustrations/32b500a948bf100b3443bc58b04303bb.png)
qui sont des approximations valides, d'où
![K_a \approx \frac{10ˆ{-pH_i} v_i[OHˆ-]_0}{v_0 [HA]_0-v_i[OHˆ-]_0}](illustrations/c7acdbbbd193a5408e54c4612a652e7c.png) , ou
, ou![K_a (v_0 \frac{[HA]_0}{[OHˆ-]_0}-v_i) \approx 10ˆ{-pH_i} v_i](illustrations/1f8cfd22bfdffad7fe9dea10405babe6.png) ou, parce que
ou, parce que ![v_e = v_0 \frac{[HA]_0}{[OHˆ-]_0}](illustrations/5e3724251c9f9d62446ef04e429343f9.png) ,
, 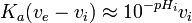 .
.
Un graphe de 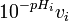 contre
contre 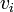 aura comme pente
aura comme pente 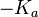 sur la région acide linéaire, et un intercepte de l'abscisse
sur la région acide linéaire, et un intercepte de l'abscisse 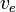 , duquel soit
, duquel soit ![[HA]_{0ˆ{ }}](illustrations/4dac97f202ae168d52a5b3ab78b02424.png) ou
ou ![[OHˆ-]_{0ˆ{ }}](illustrations/a6768ed3c004ea99b7818ac314e0f47c.png) peut être calculé. [1] La région alcaline est traitée de la même manière que pour une titrage d'un acide fort par une base forte. La Figure 2 donne un exemple; ici, les deux interceptes changent d'à-peu-près 0.2 mL, mais ceci n'est qu'un petit écart (0.5%), vu le gros volume d'équivalence.
peut être calculé. [1] La région alcaline est traitée de la même manière que pour une titrage d'un acide fort par une base forte. La Figure 2 donne un exemple; ici, les deux interceptes changent d'à-peu-près 0.2 mL, mais ceci n'est qu'un petit écart (0.5%), vu le gros volume d'équivalence.
Des équations identiques peuvent être dérivées pour un titrage d'une base faible par un acide fort. (Gran, 1952; Harris, 1998).
Contenu en carbonate
Martell et Motekaitis (1992) ont utilisé les régions les plus linéaires pour leurs graphes, puis exploité la différence entre le volume d'équivalence mesuré du côté acide et celui mesuré du côté alcalin pour ainsi estimer la quantité de CO2 absorbée par la solution alcaline. Ce processus est illustré dans la Figure 1. Dans ce cas, l'acide supplémentaire qui permet de neutraliser le carbonate, par double protonation, dans un volume 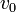 de titrate est
de titrate est ![(v_e-v_eˆ{\prime})[Hˆ+]_{0ˆ{ }} = 2v_0[CO_2]_0](illustrations/996256dcdb9e670f560448c0df504148.png) . Dans le cas opposé d'un titrage d'acide par de la base, la teneur en carbonate est calculée de façon identique avec
. Dans le cas opposé d'un titrage d'acide par de la base, la teneur en carbonate est calculée de façon identique avec ![(v_eˆ{\prime}-v_e)[OHˆ-]_{0ˆ{ }} = 2v_eˆ{\prime}[CO_2]_0](illustrations/60f7596e6644addd29d7df1f6e8aeeb9.png) , où cette fois
, où cette fois 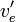 représente le volume d'équivalence mesuré du côté alcalin (d'après Martell et Motekaitis).
représente le volume d'équivalence mesuré du côté alcalin (d'après Martell et Motekaitis).
Lorsque le contenu total de CO2 absorbé est important, tel que dans les eaux naturelles et les effluents alcalins, deux ou trois inflections peuvent être décelées dans la courbe pH-volume dues aux effets tampons qu'ont le bicarbonate et le carbonate en concentrations importantes. Comme l'ont discuté Stumm et Morgan (1981), l'analyse de telles eaux peut mettre en œuvre jusqu'à six graphes de Gran à partir d'une seule titrage pour estimer les multiples points d'équivalence et mesurer l'alcalinité totale et les concentrations de carbonate et/ou de bicarbonate.
Contrôle potentiométrique de H+
Pour utiliser des mesures potentiométriques 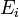 au lieu de
au lieu de 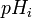 pour contrôler la concentration de
pour contrôler la concentration de 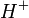 , on peut de façon triviale laisser
, on peut de façon triviale laisser ![-log_{10}[Hˆ+]_i = b_0 - b_1E_{iˆ{ }}](illustrations/8ace3adcb223ae4b60459411a2532324.png) et appliquer les équations ci-dessus, où
et appliquer les équations ci-dessus, où 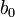 est la correction du décalage de la réponse potentiométrique
est la correction du décalage de la réponse potentiométrique 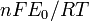 et
et 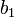 est une correction de la pente de la réponse potentiométrique
est une correction de la pente de la réponse potentiométrique 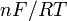 (1/59.2 unités de pH/mV à 25°C), de sorte que
(1/59.2 unités de pH/mV à 25°C), de sorte que 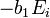 remplace
remplace 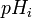 .
.
Ainsi, comme vu plus tôt pour un titrage d'acide fort par une base forte,

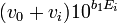 vs.
vs. 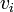 aura une région linéaire avant l'équivalence, avec pente
aura une région linéaire avant l'équivalence, avec pente ![-10ˆ{b_0}[OHˆ-]_{0ˆ{ }}](illustrations/3de0b924228585866847cb713e348e62.png)

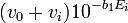 vs.
vs. 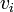 aura une région linéaire après l'équivalence, avec pente
aura une région linéaire après l'équivalence, avec pente ![10ˆ{-b_0}[OHˆ-]_0/K_{wˆ{ }}](illustrations/ba6f40ac5fa17a706f8acf5186caadea.png)
 les deux auront
les deux auront ![v_e=v_0 [Hˆ+]_0/[OHˆ-]_{0ˆ{ }}](illustrations/fa8f22bf3df8051351474ba8990a1d2d.png) comme intercepte sur x et , comme jusque là, le volume d'équivalence provenant du côté acide servira à étalloner la concentration inconnue, et la différence entre les deux volumes d'équivalence servira à estimer la teneur en carbonate
comme intercepte sur x et , comme jusque là, le volume d'équivalence provenant du côté acide servira à étalloner la concentration inconnue, et la différence entre les deux volumes d'équivalence servira à estimer la teneur en carbonate
Des graphiques analogues peuvent être fabriqués avec les données d'un titrage d'une base par de l'acide.
Calibration d'électrode
L'analyse de données potentiométriques nécessite la connaissance préalable de 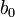 et de
et de 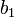 .
.
Si l'électrode est mal calibré, une correction de décalage peut être calculée in situ à partir de la pente en milieu acide :
- Pour un titrage d'un acide par de la base, la pente du côté acide est
![-[OHˆ-]_{0ˆ{ }}10ˆb](illustrations/21af90ac1c6fd99ba3ab2691deccbc04.png) , d'où
, d'où 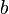 peut être calculé avec la valeur connue de
peut être calculé avec la valeur connue de ![[OHˆ-]_{0ˆ{ }}](illustrations/a6768ed3c004ea99b7818ac314e0f47c.png) ou celle provenant du volume d'équivalence.
ou celle provenant du volume d'équivalence. 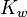 peut ensuite être calculé à partir de la pente du côté alcalin.
peut ensuite être calculé à partir de la pente du côté alcalin. - Pour un titrage d'une base par de l'acide, telle qu'illustré dans les exemples, la pente du côté acide,
![[Hˆ+]_{0ˆ{ }}10ˆb](illustrations/53b1088eb3e7a9a3b7e16c91582d816f.png) , sert pareillement à calculer
, sert pareillement à calculer 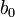 , et la pente du côté alcalin,
, et la pente du côté alcalin, ![-[Hˆ+]_{0ˆ{ }}10ˆ{-b_0}/K_w](illustrations/6d6b6359e7198c7c5e74712ad200d4db.png) permet de calculer
permet de calculer 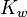 . Dans l'exemple de la Figure 1, le décalage n'était pas conséquent, car
. Dans l'exemple de la Figure 1, le décalage n'était pas conséquent, car 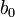 s'est avéré être -0.054 unités de pH.
s'est avéré être -0.054 unités de pH.
La valeur de 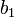 , par contre, peut dévier de la valeur théorique et ne peut être évaluée que par la calibration de l'électrode. Ceci est fréquemment effectué avec des solutions tampons aux pH connus, ou en titrant un acide fort avec une base forte, dans lequel cas une force ionique constante peut être maintenue, et
, par contre, peut dévier de la valeur théorique et ne peut être évaluée que par la calibration de l'électrode. Ceci est fréquemment effectué avec des solutions tampons aux pH connus, ou en titrant un acide fort avec une base forte, dans lequel cas une force ionique constante peut être maintenue, et ![[Hˆ{+_{ }}]_i](illustrations/2f59218efd4a9d1946146351979b9c77.png) sera connu à l'ensemble des points du titrage si
sera connu à l'ensemble des points du titrage si ![[Hˆ+_{ }]_0](illustrations/172ef49fe7646351a7adcd0a1e1044ca.png) et
et ![[OHˆ-_{ }]_0](illustrations/38ac1351a97dbf42ebca61d922c1ae9b.png) sont tous deux connus (et qui devraient être directement reliés à des étalons primaires). A titre d'exemple, Martell et Motekaitis (1992) ont calculé le pH prévu au début du titrage, ayant au préalable titré les solutions d'acide et de base contre des étalons primaires, puis ajusté le pH ainsi relevé, mais ceci ne donne pas de correction de la pente si l'une est indispensable.
sont tous deux connus (et qui devraient être directement reliés à des étalons primaires). A titre d'exemple, Martell et Motekaitis (1992) ont calculé le pH prévu au début du titrage, ayant au préalable titré les solutions d'acide et de base contre des étalons primaires, puis ajusté le pH ainsi relevé, mais ceci ne donne pas de correction de la pente si l'une est indispensable.
Suivant le travail antérieur de McBryde (1969), Gans et O'Sullivan (2000) décrivent une approche itérative pour calculer 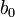 et
et 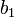 dans la relation
dans la relation ![-log_{10}[Hˆ+]_i = b_0 - b_1E_{iˆ{ }}](illustrations/8ace3adcb223ae4b60459411a2532324.png) , à partir d'un titrage d'acide fort avec une base forte :
, à partir d'un titrage d'acide fort avec une base forte :
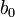 est en premier lieu estimé avec données acides selon Rossotti et Rossotti (1965), et
est en premier lieu estimé avec données acides selon Rossotti et Rossotti (1965), et 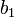 est en premier lieu donné sa valeur théorique;
est en premier lieu donné sa valeur théorique;- on trace des fonctions Gran modifiées, soit
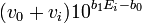 vs.
vs. 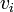 du côté acide de l'équivalence et
du côté acide de l'équivalence et 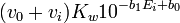 vs.
vs. 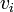 du côté alcalin, et les volumes d'équivalence
du côté alcalin, et les volumes d'équivalence 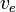 et
et 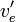 en sont calculés, comme jusque là;
en sont calculés, comme jusque là; - comme jusque là, la différence entre ces volumes d'équivalence servent à estimer le contenu en carbonate mais également pour calculer une'concentration effective'de la base
![v_e [OHˆ-]_{0ˆ{ }}/v_eˆ{\prime}](illustrations/da863bd7a2acd549312c84e9a714a79b.png) du côté alcalin de l'équivalence;
du côté alcalin de l'équivalence; - les valeurs approximatives de
![[Hˆ+]_{iˆ{ }}](illustrations/a0d788dce843b9fd9b813de4d5cc407b.png) sont calculées avec
sont calculées avec ![(v_{0ˆ{ }} [Hˆ+]_0-v_i[OHˆ-]_0)/(v_0+v_i)](illustrations/9136d4a19abbbf26fa6d0247750cee8d.png) du côté acide et avec
du côté acide et avec ![(v_e [Hˆ+]_0-v_i v_e[OHˆ-]_0 /v_eˆ{\prime})/(v_0+v_i)](illustrations/db68b7849cb90d89198a1ba5bd939ac3.png) du côté alcalin;
du côté alcalin; - la définition
![-log_{10}[Hˆ+]_i = b_0 - b_1E_{iˆ{ }}](illustrations/8ace3adcb223ae4b60459411a2532324.png) est réécrite
est réécrite ![E_{iˆ{ }} = b_0/b_1 + (1/b_1)log_{10}[Hˆ+]_i](illustrations/cf94c3bee481bea0cfdec4364e02a6a1.png) , et les données de potentiel
, et les données de potentiel 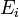 sont tracées contre
sont tracées contre ![log_{10}[Hˆ+]_{iˆ{ }}](illustrations/4a67babbe361c935555bfd70b91a39ae.png) , en utilisant les valeurs de
, en utilisant les valeurs de ![[Hˆ+]_{iˆ{ }}](illustrations/a0d788dce843b9fd9b813de4d5cc407b.png) qui correspondent aux valeurs de pH entre 2.5 et 4.5, et entre 10.7 et 11.5;[2] la méthode linéaire des moindres carrés procure alors la pente
qui correspondent aux valeurs de pH entre 2.5 et 4.5, et entre 10.7 et 11.5;[2] la méthode linéaire des moindres carrés procure alors la pente 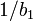 et l'intercepte
et l'intercepte 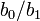 ;
; - les étapes 2 et 3 sont répétées avec les nouvelles valeurs de
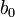 et
et 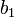 pour atteindre une plus grande précision dans le calcul des volumes d'équivalence et du contenu en CO2.
pour atteindre une plus grande précision dans le calcul des volumes d'équivalence et du contenu en CO2.
Cette procédure pourrait habituellement être modifiée pour des titrages de base par de l'acide. Le logiciel GLEE (nom dérivé de'GLass Electrode Evaluation') met en œuvre cette approche pour l'étallonage d'un électrode à partir d'un titrage d'acide fort par une base forte. Ce logiciel peut aussi calculer (par un procédé non-linéaire de moindres carrés scindé) une'correction'de la concentration de la base. L'avantage de cette méthode est que la calibration peut être conduite dans le même milieu à force ionique constante qu'on utilisera pour la détermination des constantes d'équilibre.
Il est à noter que les fonctions de Gran habituelles donnent aussi les volumes d'équivalence requis et que, comme 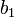 porte au départ sa valeur théorique, la valeur estimée de
porte au départ sa valeur théorique, la valeur estimée de 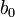 à la première étape aurait pu provenir de la pente du côté acide, tel que détaillé plus tôt. Aussi, ce procédé calcule la teneur en CO2 et peut par conséquent être combiné avec un étalonnage complet de la base, en utilisant la définition de
à la première étape aurait pu provenir de la pente du côté acide, tel que détaillé plus tôt. Aussi, ce procédé calcule la teneur en CO2 et peut par conséquent être combiné avec un étalonnage complet de la base, en utilisant la définition de 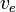 pour obtenir
pour obtenir ![[OHˆ-]_{0ˆ{ }}](illustrations/a6768ed3c004ea99b7818ac314e0f47c.png) . Finalement, la plage de pH utilisée pourrait être étendue en trouvant
. Finalement, la plage de pH utilisée pourrait être étendue en trouvant ![[Hˆ+]_{iˆ{ }}](illustrations/a0d788dce843b9fd9b813de4d5cc407b.png) par la quadratique
par la quadratique ![(v_{0{ˆ{ }}} [Hˆ+]_0-v_i[OHˆ-]_0)/(v_0+v_i) = [Hˆ+]_i - K_w/[Hˆ+]_i](illustrations/705854d77c5212c7d671721085eed406.png) .
.
Contrôle potentiométrique d'autres espèces
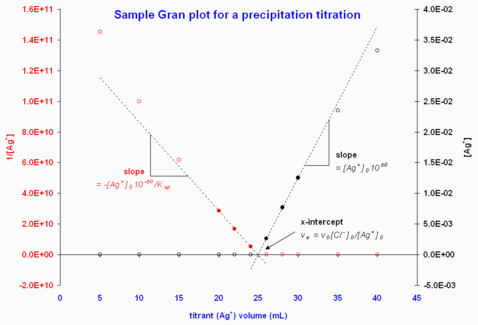
Figure 3. graphes de Gran illustratifs à partir des données d'un titrage de Cl- par Ag+ avec contrôle potentiométrique. Les potentiels ont été converties en valeurs de [Ag+]. Les cercles emplis indiquent les points retenus pour le calcul de l'intercepte par la méthode des moindres carrées donnant les courbes pointillées.
Quand on contrôle une autre espèce, disons 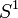 , par la potentiométrie, on peut appliquer le même formalisme avec
, par la potentiométrie, on peut appliquer le même formalisme avec ![-log_{10}[Sˆ1]_i = b_0 - b_1E_{iˆ{ }}](illustrations/e84bf6c171418f95a8de196bf3397904.png) . Alors, un titrage d'une solution d'une seconde espèce
. Alors, un titrage d'une solution d'une seconde espèce 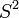 par
par 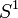 devient analogue à un titrage d'une base par de l'acide avec contrôle du pH, d'où un graphe soit de
devient analogue à un titrage d'une base par de l'acide avec contrôle du pH, d'où un graphe soit de 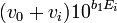 ou de
ou de 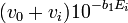 contre
contre 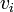 aura un intercepte sur x de
aura un intercepte sur x de ![v_0 [Sˆ0]_0 /[Sˆ1]_{0ˆ{ }}](illustrations/63f75ebe9f0d20cf06d925b6fa4dbff8.png) . Dans un titrage contraire de
. Dans un titrage contraire de 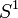 par
par 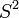 , le volume d'équivalence sera
, le volume d'équivalence sera ![v_0 [Sˆ1]_0 /[Sˆ0]_{0ˆ{ }}](illustrations/185050ed1788ea38127878cd6f004625.png) . La signification des pentes dépendra alors du type d'interaction entre les deux espèces, qu'il s'agisse d'une association ou d'une précipitation (Gran, 1952), mais, d'habitude, l'unique résultat désiré est le point d'équivalence. Cependant, la pente qui précède le point d'équivalence peut habituellement servir à mesurer le produit de solubilité
. La signification des pentes dépendra alors du type d'interaction entre les deux espèces, qu'il s'agisse d'une association ou d'une précipitation (Gran, 1952), mais, d'habitude, l'unique résultat désiré est le point d'équivalence. Cependant, la pente qui précède le point d'équivalence peut habituellement servir à mesurer le produit de solubilité 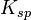 de la même façon qu'on évalue le
de la même façon qu'on évalue le 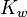 avec un titrage acide-base, quoique d'autres interactions entre paires d'ions peuvent aussi opérer. [3]
avec un titrage acide-base, quoique d'autres interactions entre paires d'ions peuvent aussi opérer. [3]
Pour illustrer ceci, prenons l'exemple d'un titrage potentiométrique de Cl- par Ag+ : 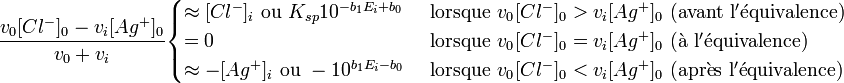
Donc,

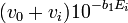 vs.
vs. 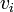 aura une région linéaire avant l'équivalence, avec pente
aura une région linéaire avant l'équivalence, avec pente ![-[Agˆ+]_010ˆ{-b_0}/K_{spˆ{ }}](illustrations/a823b3dc4380087ad7d9b224c1d2f242.png)
 et
et 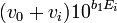 vs.
vs. 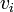 aura une région linéaire après l'équivalence, avec pente
aura une région linéaire après l'équivalence, avec pente ![[Agˆ+]_{0ˆ{ }}10ˆ{b_0}](illustrations/17e9d5eaf394597e1ff33e8544071407.png)
 dans les deux cas, l'intercepte sur x sera
dans les deux cas, l'intercepte sur x sera ![v_e=v_0 [Clˆ-]_{0ˆ{ }}/[Agˆ+]_0](illustrations/f28f4a6a774f654a527b714d7269023a.png)
La Figure 3 donne un exemple de données potentiométriques d'un tel titrage.
Comportement non-idéal
Dans toute titrage sans espèces tampons, les graphes avant et après l'équivalence devraient parfaitement croiser l'abscisse au même point, mais un comportement non-idéal peut être occasionné par des erreurs de mesures (e. g. avec un électrode mal calibré, un temps équilibration insuffisant avant d'enregistrer le potentiel, une dérive de la force ionique), des erreurs d'échantillonnage (e. g. une densité de données faible dans les régions linéaires) ou par un modèle chimique incomplet (e. g. avec la présence d'impuretés titrables telle que le carbonate dans la base, ou une précipitation incomplète lors d'un titrage potentiométrique à cause de solutions trop diluées, pour lequel cas Gran et al. (1981) propose des approches alternatives). Buffle et al. (1972) discutent de plusieurs sources de telles erreurs.
Parce que les fonctions en 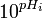 ou
ou 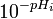 de Gran ne tendent qu'asymptotiquement vers zéro, sans jamais l'atteindre, la courbure qui résulte en approche de l'équivalence est attendue dans l'ensemble des cas. Cependant, les praticiens ne s'accordent pas sur lesquelles données utiliser pour déterminer l'équivalence, qu'il s'agisse d'utiliser les données avant ou après l'équivalence ou des deux côtés, et qu'il s'agisse d'inclure les données les plus proches de l'équivalence ou uniquement celles dans les portions les plus linéaires : [4][5] Les données les plus proches de l'équivalence feront en sorte que les deux estimations de l'intercepte sur l'axe de x seront plus coïncidants et coïncideront mieux aussi aux estimés provenant des premiers ou seconds dérivés, tandis qu'on peut présumer que les données à pH acide seront moins asujetties aux interférences provenant d'impuretés tamponeuses et titrables, telles que le bicarbonate et le carbonate dans la base (voir Contenu en carbonate), mais aussi de l'effet d'une force ionique dérivante. Dans les graphiques donnés ici en exemples, les régions les plus linéaires (les données représentées par les cercles emplis) étaient celles choisies pour le traitement par la méthode des moindres carrés donnant les pentes et interceptes. La sélection des données à retenir est toujours subjective.
de Gran ne tendent qu'asymptotiquement vers zéro, sans jamais l'atteindre, la courbure qui résulte en approche de l'équivalence est attendue dans l'ensemble des cas. Cependant, les praticiens ne s'accordent pas sur lesquelles données utiliser pour déterminer l'équivalence, qu'il s'agisse d'utiliser les données avant ou après l'équivalence ou des deux côtés, et qu'il s'agisse d'inclure les données les plus proches de l'équivalence ou uniquement celles dans les portions les plus linéaires : [4][5] Les données les plus proches de l'équivalence feront en sorte que les deux estimations de l'intercepte sur l'axe de x seront plus coïncidants et coïncideront mieux aussi aux estimés provenant des premiers ou seconds dérivés, tandis qu'on peut présumer que les données à pH acide seront moins asujetties aux interférences provenant d'impuretés tamponeuses et titrables, telles que le bicarbonate et le carbonate dans la base (voir Contenu en carbonate), mais aussi de l'effet d'une force ionique dérivante. Dans les graphiques donnés ici en exemples, les régions les plus linéaires (les données représentées par les cercles emplis) étaient celles choisies pour le traitement par la méthode des moindres carrés donnant les pentes et interceptes. La sélection des données à retenir est toujours subjective.
Littérature citée
- Buffle, J., Parthasarathy, N. et Monnier, D. (1972) : Errors in the Gran addition method. Part I. Theoretical Calculation of Statistical Errors; Anal. Chim. Acta 59, 427-438; Buffle, J. (1972) : Anal. Chim. Acta 59, 439.
- Butler, J. N. (1991) : Carbon Dioxide Equilibria and Their Applications; CRC Press : Boca Raton, FL.
- Butler, J. N. (1998) : Ionic Equilibrium : Solubility and pH Calculations; Wiley-Interscience. Chap. 3.
- Gans, P. et O'Sullivan, B. (2000) : GLEE, a new computer program for glass electrode calibration; Talanta, 51, 33–37.
- Gran, G. (1950) : Determination of the equivalence point in potentiometric titrages, Acta Chem. Scand. , 4, 559-577.
- Gran, G. (1952) : Determination of the equivalence point in potentiometric titrages-- Part II, Analyst, 77, 661-671.
- Gran, G., Johansson, A. et Johansson, S. (1981) : Automatic titrage by Stepwise Addition of Equal Volumes of Titrant Part VII. Potentiometric Precipitation titrages, Analyst, 106, 1109-1118.
- Harris, D. C. : Quantitative Chemical Analysis, 5th Ed. ; W. H. Freeman & Co., New. York, NY, 1998.
- Martell, A. E. et Motekaitis, R. J. : The determination and use of stability constants, Wiley-VCH, 1992.
- McBryde, W. A. E. (1969) : Analyst, 94, 337.
- Rossotti, F. J. C. et Rossotti, H. (1965) : J. Chem. Ed., 42, 375
- Skoog, D. A., West , D. M., Holler, F. J. et Crouch, S. R. (2003) : Fundamentals of Analytical Chemistry : An Introduction, 8th Ed., Brooks and Cole, Chap. 37.
- Stumm, W. et Morgan, J. J. (1981) : Aquatic chemistry, 2nd Ed. ; John Wiley & Sons, New York.
Notes
- Si la force ionique n'est pas constante, on peut modifier cette expression pour un quotient d'activité changeant. Voir Harris (1998) ou ce document en ligne. Consulté le 2008-02-17
- Pour un électrode de verre, ces plages de pH sont les régions de linéarité qui évitent la variation des potentiels de jonction et/ou l'erreur alcaline aux extrêmes de pH, et qui de surcroît évitent les erreurs de mesure près de l'équivalence mais aussi les erreurs de calcul dues aux mises à l'écart de
![[OHˆ-]_{iˆ{ }}](illustrations/8a2546fe03c397e8fe08c9705ab50965.png) du côté acide et de l'équilibre carbonate/bicarbonate du côté alcalin.
du côté acide et de l'équilibre carbonate/bicarbonate du côté alcalin. - Gran et al. (1981) traite plus longuement de ce sujet, tenant compte des autres espèces complexes générées dans les titrages de Cl- par Ag+ (Ag2Cl+ et AgCl2-, surtout), mais aussi dans d'autres titrages avec précipitation, pour calculer les volumes d'équivalence lorsque les concentrations sont faibles et la précipitation incomplète.
- Les instructions apportées aux étudiants témoignent des différentes pratiques recommandées. A titre d'exemple, C. Chambers de l'université George Fox recommande d'utiliser les données du côté acide "juste avant" le point d'équivalence dans les titrages acide-base (document en ligne. Consulté le 2008-02-17). Suivant Harris (1998), M. El-Koueidi et M. Murphy de l'université de la Caroline du Nord à Charlotte (document en ligne. Consulté le 2008-03-22) et W. Wolbach de l'université Depaul (document en ligne. Consulté le 2008-02-17) recommandent l'utilisation des derniers 10-20% des données précédant l'équivalence, et Wolbach reconnaît que les données du côté alcalin peuvent aussi servir à mesurer le contenu en CO2 de la base. De manière identique, W. E. Brewer et J. L. Ferry de l'université de la Caroline du Sud recommandent d'utiliser les données devançant de 10% l'équivalence (document en ligne. Consulté le 2008-02-17). K. Kuwata de l'université Macalester College recommande à ses étudiants de choisir la quelconque portion de données avant l'équivalence qui donne la ligne la plus droite (document en ligne. Consulté le 2008-02-17). D. L. Zellmer de l'université California State à Fresno demande aux étudiants d'utiliser les données de part et d'autre de l'équivalence, mais celles les plus éloignées du point d'équivalence, et d'évaluer les erreurs pour ainsi déterminer si les deux estimations du volume d'équivalence changent de façon importante (données pH : document en ligne. Consulté le 2008-02-17; titrage potentiométrique de chlorure par l'ion d'argent : document en ligne. Consulté le 2008-02-17).
- Butler (1991) discute du problème de la sélection de données, et examine aussi les interférences provenant d'impuretés comme le borate et le phosphate.
Bibliographie
- L. Lopes Linéarisations de type Gran
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 30/11/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

![K_{wˆ{ }} = [Hˆ+]_i[OHˆ-]_i](illustrations/d5d8e4c93454a77e03626b65ab8d2943.png)

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité