Détermination des constantes d'équilibre
Les constantes d'équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques.
Les constantes d'équilibre sont évaluées pour quantifier les équilibres chimiques à partir de mesures de concentrations, directes ou indirectes, et mettant en œuvre des techniques numériques.
Cet article se limite aux équilibres en solutions entre solutés pour lesquels l'activité chimique est mesurée par la concentration molaire en mol L-1. Destiné aux praticiens spécialisés ainsi qu'aux apprentis ayant une appréciation de base des équilibres chimiques, cet article traite du sujet en profondeur jusqu'à permettre la programmation des techniques de détermination en se souciant de la rigueur statistique, et s'attarde à l'interprétation objective des résultats.
Introduction
Un équilibre chimique peut s'écrire généralement
où on distingue les réactifs A, B, ... , à gauche de la double flèche, des produits P, Q, ... à sa droite. On peut s'approcher de l'équilibre des deux directions, et cette distinction entre réactifs et produits n'est que conventionnelle. La double flèche indique un échange dynamique, plus ou moins rapide, entre réactifs et produits, et l'équilibre est atteint quand les concentrations des espèces participantes deviennent constantes. Le rapport des produits des concentrations, généralement représenté par K et nommé la constante d'équilibre, s'écrit conventionnellement avec les réactifs au dénominateur et produits au numérateur ainsi
![K = \frac {[P]ˆp[Q]ˆq...}{[A]ˆa[B]ˆb...}](illustrations/91ec2ac7e5a263db661a81cf2d078bfa.png) ,
,
Ce rapport sera alors constant à une température donnée, pourvu que le quotient des activités chimiques est constant, supposition qui sera valide à une force ionique élevée, faute de quoi ce seront les activités qu'il faudra évaluer. Il exprime la position de l'équilibre, plus ou moins favorable (K > 1) ou défavorable (K < 1), qu'on peut quantifier si on peut mesurer la concentration de l'une des espèces en équilibre, avec l'aide des quantités analytiques (concentrations, masses ou volumes) des réactifs mis en œuvre.
Plusieurs types de mesures sont envisageables. Cet article touche les trois types essentiellement utilisés et leurs limitations. Plusieurs autres, plus rares, sont décrits dans l'œuvre classique de Rossotti et Rossotti[1].
Sauf s'il s'agit d'un dispositif expérimental particulièrement simple, les rapports entre les constantes d'équilibre et les concentrations mesurées seront non-linéaires. Avec un ordinateur rapide et un logiciel équipé, et ayant une quantité suffisante de mesures de concentration, la détermination d'un nombre indéfini de K, impliquant un nombre indéfini d'espèces en solution, se fait aisément et de manière statistiquement rigoureuse par solution numérique des rapports non-linéaires qui décrivent un dispositif d'équilibres enchevêtrés. Cette détermination suit alors le parcours d'une modélisation, avec trois étapes : l'articulation d'un modèle, sa numérisation et son affinement. Cet article détaille ces trois étapes et finit par proposer certains logiciels utiles.
Mesures expérimentales
La détermination de constantes d'équilibre se fait depuis plusieurs décennies et les techniques utilisées ont énormément évolué et sont devenues de véritables spécialités. Ce résumé ne peut pas donner l'ensemble des détails nécessaires à l'acquisition de mesures valables, et le lecteur se reportera aux textes spécialisés pour ce faire.
Potentiométrie et pH-métrie
La concentration de certaines espèces peut être mesurée avec électrodes spécialisées, telles que l'électrode de verre indicatrice du pH (pour mesurer [H+]) ou les électrodes sélectives (de verre ou à membrane) pour certains autres ions[2]. Ces électrodes devront être calibrées avec des solutions de référence à concentration fixe.
Pour les mesures de pH[3], des solutions-tampons seront utilisées et les lectures du pH-mètre obéiront
- pH = nF / RT (E0 − E) ,
expression dérivée de l'équation de Nernst, où E0 est le potentiel standard de l'électrode, E est la mesure potentiométrique, n est le nombre d'électrons impliqués (= 1), F est la constante de Faraday, R est la constante de gaz parfait et T représente la température (en kelvin). Chaque unité de pH génère une différence de potentiel d'environ 59 mV à 298 K. La méthode de Gran peut, avec une titration acide fort-base forte, servir de calibration et détecter la présence de carbonates dans un titrant à base d'hydroxyde.
Pour toutes mesures potentio- ou pH-métriques, une calibration simple peut se faire avec l'équation de Nernst modifiée
- E = a + blog10[A]
où A représente l'espèce détectée par l'électrode. Au minimum deux mesures, depuis au moins deux concentrations de référence, suffisent pour établir les paramètres empiriques a et b donnant la possibilité d'ainsi de convertir les potentiels en concentrations.
Le nombre de données doit égaler ou excéder le nombre de constantes d'équilibre à déterminer, ce qui est facile avec une titration.
Limitations
Des valeurs de constantes d'équilibre entre à peu près 102 et 1011 peuvent être mesurées directement par potentiométrie avec électrodes de verre, grâce à la réponse logarithmique de ces électrodes. La méthode par compétition peut étendre cette plage, mais l'équation de Nernst tient mal à particulièrement bas ou particulièrement haut pH.
Spectrométrie électronique
L'absorbance à une longueur d'onde dans la région visible ou de l'ultraviolet doit obéir la loi de Beer-Lambert, où il existe un rapport linéaire entre la mesure et la concentration de l'espèce mesurée, soit
où 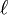 est la longueur du chemin optique,
est la longueur du chemin optique, 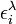 est l'absorptivité molaire (le cœfficient d'extinction molaire) à chemin optique unitaire à la longueur d'onde λ de l'i ème espèce chromophore à concentration ci. Cette formulation reconnaît que, sauf les cas simples, plusieurs espèces peuvent absorber la lumière à une même longueur d'onde, ce qui nécessite la détermination simultanée de la concentration et de ελ pour chaque espèce.
est l'absorptivité molaire (le cœfficient d'extinction molaire) à chemin optique unitaire à la longueur d'onde λ de l'i ème espèce chromophore à concentration ci. Cette formulation reconnaît que, sauf les cas simples, plusieurs espèces peuvent absorber la lumière à une même longueur d'onde, ce qui nécessite la détermination simultanée de la concentration et de ελ pour chaque espèce.
Puisqu'avec une seule mesure, il n'est pas envisageable de déterminer plus qu'un paramètre, il faut avoir soit pour un même échantillon des mesures d'absorbance à plusieurs longueurs d'onde qui dépendront d'une même valeur de la constante d'équilibre pour ainsi cerner l'ou les ε inconnus, soit plusieurs échantillons à différentes concentrations relatives en réactifs dont les mesures d'absorbance dépendront des mêmes valeurs d'ε à la même longueur d'onde pour ainsi cerner la constante d'équilibre inconnue, soit plusieurs échantillons examinés à plusieurs longueurs d'onde. On aura NCNλ mesures d'absorbance provenant de NC solutions (à concentrations relatives différentes) mesurées à Nλ longueurs d'onde, pour évaluer au pire NE (Nλ + 1) inconnus provenant de NE espèces chromophores associées à NENλ valeurs d'ε et NE constantes d'équilibre. Il serait par conséquent souhaitable d'obtenir indépendamment les valeurs d'ε des réactifs isolés (et/ou des produits isolés) et/ou d'évaluer indépendamment, si envisageable, certaines des constantes d'équilibre, pour ainsi diminuer le nombre total d'inconnus par détermination. De toute façon, il faut s'organiser pour avoir tout autant (ou plus) de données que d'inconnus (au pire NCNλ ≥ NE (Nλ + 1) ). On se limite généralement à un petit nombre de longueurs d'onde choisies pour bien répondre aux changements des concentrations des espèces chromophores, en particulier aux λmax des réactifs purs ou produits isolés.
Limitations
C'est une technique utilisée en particulier en chimie de coordination avec les métaux de transition. Une limite supérieure sur K de 104 est habituel, correspondant à la précision des mesures, mais cette limite dépend aussi de l'intensité de l'absorption. Parfaitement, les spectres du réactif et du produit sont bien différents; un chevauchement important nécessite une attention spécifique. Soit qu'on obtiendra aussi les spectres individuels du réactif et/ou du produit pour limiter la plage de calcul, et par conséquent les valeurs ε seront connues pour les espèces limitantes, soit le calcul effectuera par là-même une déconvolution du spectre, calcul dangereux à cause de la quantité des ε à déterminer pour obtenir une seule constante d'équilibre.
Spectrométrie par RMN
Cette technique se limite à de cas d'échanges entre espèces assez simples (par exemple, échanges entre isomères ou entre ligand et complexes), où les noyaux observés changent d'environnement chimique suite à l'échange. À l'idéal, il faut des signaux (préférablement des singulets) bien résolus (sans chevauchement).
S'il s'agit d'un équilibre lent, sur l'échelle de temps du phénomène rmn[note 1] entre deux espèces détectables simultanément, le rapport de la mesure d'intégration des signaux de chaque espèce suffit à établir le rapport de concentration entre les deux, pourvu qu'on prenne les soins nécessaires à la mesure précise de l'intégration[note 2], d'où des mesures à différentes concentrations pourront quantifier la constante d'équilibre entre les deux.
Sinon et généralement dans les situations de complexation, lorsque l'équilibre est rapide sur l'échelle RMN, on observe un seul signal par type de noyau pour les espèces en équilibre. Le déplacement chimique de ce genre de signal est alors perçu par l'instrument comme la moyenne 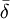 des états contribuants, c'est-à-dire la moyenne des signaux provenant des noyaux participants, généralement[note 3] pondérée par leurs concentrations c (ou plus exactement par leurs fractions molaires),
des états contribuants, c'est-à-dire la moyenne des signaux provenant des noyaux participants, généralement[note 3] pondérée par leurs concentrations c (ou plus exactement par leurs fractions molaires),
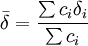 .
.
Plusieurs signaux divers, provenant de noyaux divers dans un même échantillon, peuvent ainsi être soumis au même traitement numérique pour déterminer avec d'avantage de confiance les mêmes constantes d'équilibre. Autrement, plusieurs rapports stœchiométriques seront mesurés.
On aura par conséquent, dans un dispositif d'échange rapide, NCNS mesures de déplacement chimique provenant de NS signaux avec NC échantillons aux concentrations relatives différentes pour évaluer au pire NE (NS + 1) inconnus, soit les déplacements δi des NS signaux des NE espèces en équilibre et NE constantes d'équilibre K. Les valeurs de δ des noyaux dans les espèces limitantes (réactif pur et/ou produits purs) peuvent fréquemment être déterminées séparément pour limiter la détermination aux valeurs δ et K autrement inconnaissables et par conséquent diminuer le nombre de valeurs inconnues, mais de toute façon il faut s'organiser pour avoir tout autant ou plus de données que d'inconnues (au pire NCNS ≥ NE (NS + 1) ).
Limitations
Cette méthode est limitée aux molécules diamagnétiques comprenant un noyau sensible et , ce, soit bien en dessous ou bien au-dessus de la température de coalescence du phénomène d'échange observé. Les déplacements chimiques de référence (par exemple, du réactif isolé, dans une situation de complexation) doivent être obtenus à la même température et dans le même solvant que le mélange contenant un complexe. La précision des mesures de déplacements chimiques convient aux valeurs de K à déterminer allant jusqu'à à peu près 104, quoique la méthode de compétition peut étendre cette plage.
Méthodes de calcul
Les données de base incluront pour chaque échantillon les concentrations analytiques des réactifs mis ensemble pour former les espèces complexes en équilibre entre eux et avec les réactifs libres, ainsi qu'une mesure de la concentration d'une espèce ou de plusieurs espèces. Le nombre de mesures sera préférablement supérieur (et au minimum égal) au nombre de valeurs inconnues (constantes d'équilibre en cause, mais aussi les valeurs d'ε ou de δ à déterminer). Moins on aura d'inconnues à déterminer à la fois, plus chaque détermination sera fiable.
Linéarisations dangereuses
Une détermination graphique est quelquefois envisageable avec un dispositif expérimental simple impliquant un ou deux équilibres. Cela nécessite une linéarisation avec ou sans approximations des rapports non-linéaires entre constantes d'équilibre et les concentrations mesurées, d'où on soutirera la valeur du ou des K avec la pente ou l'intercepte ou avec une combinaison des deux. Il va sans dire que toute approximation amoindrira la généralité de la détermination. Même si on peut obtenir les valeurs exactes de la pente et de l'intercepte par calcul (méthode des moindres carrés) plutôt que par estimation visuelle, ce genre de détermination peut violer un principe de base en statistique des modèles linéaires[4], soit que la distribution des erreurs de mesure (erreurs affligeant les y dans un rapport linéaire y = mx + b) sera aléatoire ainsi qu'à distribution normale des amplitudes[note 4]. Quoiqu'on puisse s'attendre à ce que les erreurs de mesure obéiront une distribution normale, ce ne sera pas le cas des fonctions de ces mesures qui résulteront d'une linéarisation des équations régissant les équilibres en cours.
En guise d'exemple, l'équation de Henderson-Hasselbalch est une linéarisation courante pour quantifier un équilibre simple. Elle est parfois utilisée de manière statistiquement rigoureuse ou dangereuse. Dans le cas d'une titration d'acide faible HA avec une solution d'hydroxyde, on propose le modèle
où un volume vi de solution d'hydroxyde à teneur [OH − ]0 est livrée à une solution d'acide à teneur d'origine [HA]0 pour ensuite mesurer le pHi résultant. Cette équation a la forme
Puisqu'ici on oppose la mesure elle-même (le pHi) aux paramètres connus (les constantes [HA]0 et [OH − ]0 et la variable vi), la détermination du pKa sera rigoureuse, pourvu qu'on ne calcule pas de pente chimérique (voir plus bas).
Par contre, un cas opposé fait partie des travaux pratiques d'un cours de chimie d'une université américaine[5]. C'est une détermination spectrométrique du pKa d'un indicateur I, 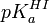 , par double application de l'équation de Henderson-Hasselbalch. On mesure l'absorbance
, par double application de l'équation de Henderson-Hasselbalch. On mesure l'absorbance 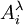 à une ou plusieurs longueurs d'onde λ d'une solution à teneur totale en I de [I]0 lors d'une titration avec de l'hydroxyde à teneur [OH − ]0, et la première application de l'équation de Henderson-Hasselbalch oppose le
à une ou plusieurs longueurs d'onde λ d'une solution à teneur totale en I de [I]0 lors d'une titration avec de l'hydroxyde à teneur [OH − ]0, et la première application de l'équation de Henderson-Hasselbalch oppose le 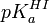 à l'absorbance, soit
à l'absorbance, soit
Mais le pH n'est pas contrôlé directement; plutôt, on le calcule avec la seconde application de l'équation de Henderson-Hasselbalch, tout en connaissant le pKa d'un tampon HA, 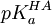 , mais aussi la concentration d'origine du tampon, [HA]0, ce qui donne
, mais aussi la concentration d'origine du tampon, [HA]0, ce qui donne
On y reconnaîtra la forme
analogue à celle du premier exemple.
Le fait qu'il y ait double application de l'équation de Henderson-Hasselbalch n'est pas problématique. Le problème est que ce n'est pas la mesure Aλ qui est opposée aux paramètres connus, mais bien une fonction non-linéaire de la mesure, plus exactement une différence de fonctions logarithmiques,
![y=\log_{10} \lbrace A_iˆ{\lambda}-\epsilon_{HIˆ+}ˆ{\lambda}\ell[I]_0 \rbrace-\log_{10} \lbrace \epsilon_{I}ˆ{\lambda}\ell[I]_0-A_iˆ{\lambda} \rbrace](illustrations/d2fbc8fc3852384528498076c9185ba3.png) .
.
Bien qu'on peut espérer une distribution aléatoire des erreurs de mesure Aλ et que l'amplitude de ces erreurs obéira une distribution normale, ce ne sera sans doute pas le cas chez la quantité complexe y même si les ε et le [I]0 sont sans erreur envisageable, ce qui n'est pas le cas. Au contraire, cette détermination imposera une distribution aléatoire des résidus 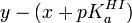 et les amplitudes de ces résidus obéiront une distribution normale, mais il n'y a aucune signification physique ni dans la quantité y, ni dans les
et les amplitudes de ces résidus obéiront une distribution normale, mais il n'y a aucune signification physique ni dans la quantité y, ni dans les 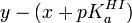 .
.
Un autre problème survient avec ces deux exemples : un expérimentaliste mal avisé verra dans la relation y = x + pKa un modèle linéaire de forme générale y = mx + b et aura le réflexe de calculer une pente et un intercepte par la méthode des moindres carrés, fréquemment avec une fonction préconstruite d'un logiciel (par exemple Excel de Microsoft) [note 5]. tandis qu'il n'y a pas de pente à déterminer. Non seulement la valeur du pKa ainsi calculé ne sera pas justifiable, les statistiques de confiance dans le résultat, basées sur une détermination de deux inconnues, seront alors faussées. Le pKa n'est pas en fait un intercepte à déterminer en extrapolant vers x = 0, mais la simple moyenne des différences y − x, et la confiance en la valeur du pKa ainsi obtenue sera donnée par la déviation standard autour de cette moyenne. La tentation de déterminer un pente chimérique est d'autant plus grande que la déviation standard du pKa calculé avec une pente sera plus petite, puisque la modélisation d'une relation avec deux paramètres (pente et intercepte) sera encore plus satisfaisante qu'avec un seul paramètre (l'intercepte, dans le cas présent).
Modélisation non-linéaire
Lorsque un dispositif met en œuvre plusieurs équilibres ou lorsque les équilibres mettent en cause plusieurs espèces chimiques à la fois, une linéarisation devient impossible sans y imposer des restrictions (approximations). Même si on se conforme aux exigences d'un modèle linéaire, toute restriction rend la détermination approximative et moins générale. C'est tandis qu'un traitement numérique s'impose.
Dans l'exemple ci-haut, où la linéarisation ne donnait pas un modèle linéaire valide, on aurait dû s'en tenir à une relation f non-linéaire
En général, on travaille avec une relation
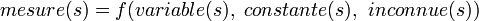 .
.
On ne peut pas trouver les inconnues par solution directe. De toute façon, l'équation ne sera pas exacte, étant donné qu'il y aura des erreurs de mesure, des erreurs dans les variables, des erreurs systématiques dans les constantes et la possibilité que les paramètres inconnus ne suffiront pas ou ne seront pas les plus justes. Plutôt, on écrit
- mesure (s) = calcul (s) + erreur.
où les calcul (s) sont obtenus avec 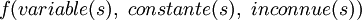 . On cherchera le meilleur modèle f (en général, on ne s'attarde qu'aux paramètres inconnus lorsque on modélise, mais le modèle entier comprend l'ensemble des paramètres) qui apportera les moindres résidus (mesure − calcul) . Pour ce faire, il faut avoir au départ des estimations des valeurs inconnues et parfaire ces estimations par itération algorithmique jusqu'à ce que les résidus (mesure − calcul) soient amoindries — la méthode des moindres carrés assurera en même temps une distribution normale des résidus — pour en arriver à ainsi déterminer les valeurs inconnues au sein du modèle, avec une appréciation des erreurs de la détermination. Par la suite, on pourra songer à modifier le modèle, s'il y a lieu, et comparer différents modèles de manière rigoureuse.
. On cherchera le meilleur modèle f (en général, on ne s'attarde qu'aux paramètres inconnus lorsque on modélise, mais le modèle entier comprend l'ensemble des paramètres) qui apportera les moindres résidus (mesure − calcul) . Pour ce faire, il faut avoir au départ des estimations des valeurs inconnues et parfaire ces estimations par itération algorithmique jusqu'à ce que les résidus (mesure − calcul) soient amoindries — la méthode des moindres carrés assurera en même temps une distribution normale des résidus — pour en arriver à ainsi déterminer les valeurs inconnues au sein du modèle, avec une appréciation des erreurs de la détermination. Par la suite, on pourra songer à modifier le modèle, s'il y a lieu, et comparer différents modèles de manière rigoureuse.
Le problème de la minimisation des résidus n'est qu'un problème technique et il existe plusieurs algorithmes qui se vantent certains avantages. Tous doivent arriver à la même conclusion sur un même modèle décrivant un même dispositif. Cet article cherche moins à comparer les diverses méthodes numériques qu'à assurer une approche statistiquement valide, approche qui pourra alimenter une programmation des calculs.
La méthode décrite ici suit le cheminement de Alcock et al. (1978) pour un régime général d'équilibres multiples.
Le modèle chimique
Le modèle chimique doit inclure l'ensemble des espèces en équilibre de sorte à permettre un calcul de chacune de leur concentration, impliquant tout autant d'équilibres qu'il y a d'espèces en solution[note 6]. Il y a deux genres de constantes d'équilibre utilisés pour ce faire : les constantes générales et les constantes de formation cumulative.
Une constante dite générale gouverne un équilibre entre n'importe quelles espèces, par exemple un équilibre d'échange de ligands entre deux complexes de coordination, par exemple
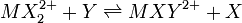 où
où ![K = [MXYˆ{2+}][X]/[MX_2ˆ{2+}][Y]](illustrations/f8c305c4e75709f3e222db6e051cf41c.png)
Une constante de formation cumulative se limite à un équilibre entre une espèce et les réactifs irréductibles qui la forment par cumul. Comme tout ensemble en équilibre survient après avoir mélangé des réactifs, on définit par conséquent toute espèce comme le résultat ApBq... d'une combinaison stoichiométrique et unique des réactifs irréductibles A, B, ...
spécifiée par les cœfficients de stœchiométrie p, q, ... , et la constante d'équilibre qui régit cette formation est généralement symbolisé par un β, ainsi
Ce faisant, nous garantissons tout autant de constantes que d'espèces et aucun équilibre ne sera redondant. Même les réactifs irréductibles peuvent être représentés de la même manière, avec des β symboliques,
![[A]ˆ{ _{ }} = \beta_{10...}[A]ˆ1[B]ˆ0...](illustrations/a03b831a12836bea2c8f89fcb1e6819d.png) où
où ![\beta_{10...ˆ{}} ={[A_1B_0...]}/{[A]ˆ1[B]ˆ0...}=1](illustrations/3d5a7390dad2c80b28c3a63554ff987c.png)
![[B]ˆ{ _{ }} = \beta_{01...}[A]ˆ0[B]ˆ1...](illustrations/840da526829a995334bfbad65d128230.png) où
où ![\beta_{01...ˆ{}} ={[A_0B_1...]}/{[A]ˆ0[B]ˆ1...}=1](illustrations/a0f07c670b545899915b36750ec97145.png)

pour que l'ensemble des espèces soient traitées de façon homogène. De façon générale, la concentration de la i ième espèce Ei, constituée d'une combinaison de NR réactifs R, est
où le cœfficient de stœchiométrie ai, k est le nombre d'équivalents du k ième réactif entrant dans la formation de la i ième espèce, et où βi est la constante d'équilibre qui régit cet assemblage. Cette représentation harmonisée favorisera la notation à venir et la programmation des logiciels.
Il s'avère que cette deuxième sorte d'équilibre est d'utilité tout aussi générale que la première. En effet, tout ensemble d'espèces en équilibres multiples pourra être modelé avec équilibres de formation (bien qu'ils ne seront pas forcément le meilleur choix) [note 7] et , une fois le dispositif d'équations résout et les β déterminés, tout autre équilibre ne sera qu'une combinaison de ces mêmes équilibres de formation, et toute autre constante ne sera qu'une combinaison de ces mêmes β et pourra par conséquent être quantifié ensuite (voir constantes dérivées). Pour reprendre l'exemple d'échange de ligands entre complexes de coordination cité ci-haut, nous pouvons écrire
![K = [MXYˆ{2+}][X]/[MX_2ˆ{2+}][Y] = \beta_{111} \beta_{010}/\beta_{120} \beta_{001}](illustrations/523da32fcddb2a7352f94ac146e0db8a.png)
- où
![\beta_{111} = \frac{[MXYˆ{2+}]}{[Mˆ{2+}][X][Y]}](illustrations/e9df1dbea9debbc44c4e3612ed6a9144.png) ,
, ![\beta_{120} = \frac{[MX_2ˆ{2+}]}{[Mˆ{2+}][X]ˆ2[Y]ˆ0}](illustrations/ec946c6f6054f1438723f18c8e029115.png) ,
, ![\beta_{010} = \frac{[X]}{[Mˆ{2+}]ˆ0[X][Y]ˆ0}(=1)](illustrations/aa0920f5a0162daf2f6ebbdce919b3d4.png) et
et ![\beta_{001} = \frac{[Y]}{[Mˆ{2+}]ˆ0[X]ˆ0[Y]} (=1)](illustrations/76e5856a377a36696bebdd2f3c188da5.png)
Le grand avantage d'une telle formulation avec équilibres de formation est que le calcul des concentrations (section suivante) est largement simplifié.
Dans l'ensemble des cas, si l'expérience est conduite en milieu aqueux, il faudra inclure la dissociation de l'eau (son autoprotolyse)
et imposer la valeur du produit ionique KW appropriée à la situation[6] comme constante connue. Si H + or OH − est un des réactifs, disons A, la dissociation de l'eau peut être représentée en utilisant la même notation que celle des équilibres de formation, par
![\beta_{-10...ˆ{ }}= K_w = {[OHˆ-]}/{[Hˆ+]ˆ{-1}[B]ˆ0...}](illustrations/fe0fa4df62e79682a9e2025f08e2d24b.png) si H + est le réactif A, ou
si H + est le réactif A, ou ![{[Hˆ+]}/{[OHˆ-]ˆ{-1_{ }}[B]ˆ0...}](illustrations/c634aada6e226e0df6a1a6111386b7aa.png) si OH − est le réactif A.
si OH − est le réactif A.
Si jamais la valeur du KW n'était pas réputé pour la situation expérimentale voulue, par exemple dans un mélange de solvants spécifique et (ou) à une température spécifique, on pourrait la considérer comme quantité inconnue à déterminer en même temps que les autres constantes inconnues, mais il serait plus sage de la déterminer jusque là, indépendamment, par exemple par la méthode de Gran, pour limiter le nombre d'inconnus à traiter par expérience et la corrélation entre les résultats.
Il va sans dire que le modèle doit être complet, dans le sens que doivent y paraître l'ensemble des équilibres enchevêtrés qui risquent d'agir sur la mesure. Cependant, il est courant d'omettre du modèle les espèces qu'on anticipe n'exister qu'en concentrations négligeables, par exemple les équilibres mettant en cause l'électrolyte qu'on ajoutera pour maintenir une force ionique constante ou les espèces-tampons qui maintiendront un pH constant. Après avoir numérisé les équilibres et jugé du succès de la modélisation, on aura l'occasion de revoir la pertinence des espèces incluses et l'obligation d'y inclure des espèces non-anticipées.
Numérisation
À un ensemble de β correspondra un ensemble unique de concentrations, parce qu'elles sont bornées par les quantités des matériaux utilisées.
La quantité de chaque réactif mis en réaction, désormais dispersée parmi l'ensemble des espèces complexes qu'il forme ainsi qu'en forme libre, restera constante dans un échantillon donné, et sera par conséquent connue dans chaque échantillon (ou à chaque étape d'une titration) selon les volumes et les concentrations des stocks mélangés pour préparer l'échantillon. Pour chaque réactif R, on aura par conséquent une concentration analytique connue [R]connue dans chaque échantillon. On cherchera alors les concentrations de l'ensemble des espèces constituées par ce réactif, mais aussi le reste inutilisé du réactif (réactif libre), de sorte que le total de leurs parts en R, [R]calc, soit égal à [R]connue. La somme des parts du j ième de NR réactifs formant les NE espèces E, s'écrit
où le cœfficient stœchiométrique ai, j indique le nombre d'équivalents du j ième réactif contenu dans l'i ième espèce. Ainsi, l'unicité des valeurs des concentrations pour chaque ensemble de β est assuré par les NR [R]connue correspondant aux NR'inconnus'[Rk].
La détermination trouvera par conséquent l'unique ensemble des β qui fixeront les concentrations des espèces qui reproduiront le mieux les mesures expérimentales et il suffira d'avoir au moins tout autant de mesures que de β inconnus.
La stratégie à suivre consiste par conséquent à
- calculer les concentrations estimées des NE espèces E en calculant les concentrations estimées des NR réactifs libres R à partir d'estimations des valeurs des β inconnus[6], ce qui requiert que les [R]calc et les [R]connue soient mis en accord par ajustement des [Rk] de manière itérative
- comparer la mesure à ce que les concentrations ainsi estimées permettent d'anticiper, c'est-à-dire comparer la mesure réelle à celle estimée, selon le rapport entre la quantité mesurée et les concentrations dont la mesure dépend
- calculer et appliquer un ajustement aux valeurs des β inconnus
- recalculer les concentrations des réactifs libres
- re-comparer les mesures réelles et estimées
- ré-ajuster les β inconnus
- et ainsi de suite de manière itérative, jusqu'à ce que l'accord des mesures réelles et estimées ne puisse plus être perfectionné, nous servant à conclure que les β auront par conséquent été déterminés.
Calcul des concentrations
À chaque itération de la détermination, les concentrations doivent être calculées, mais il n'est pas envisageable de résoudre directement les NR équations parallèles
- [Rj]connue = [Rj]calc
parce qu'elles ne sont pas linéaires. Plutôt, la méthode Gauss-Newton est adoptée, où on se rapprochera progressivement de la solution à partir d'un début approximatif où auront été estimées les concentrations [R]. À la μ ième itération, on calculera des corrections Δ[Rk]μ à apporter aux valeurs en cours [Rk]μ pour générer de meilleures estimations des [Rj]calc et qui serviront à la (μ + 1) ième itération. Ces corrections proviendront de la solution des séries de Taylor (tronquées pour ne retenir que les termes de premier ordre) [note 8]
que on peut rassembler en notation matricielle-vectorielle ainsi
où le (j, k) ième élément de la matrice 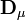 sera le dérivé
sera le dérivé ![{\partial [R_j]_{\mu}ˆ{calc}}/{\partial [R_k]}](illustrations/349f4e2f69b383b7bfb23145a0334047.png) [note 9] alors que le vecteur
[note 9] alors que le vecteur 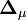 contiendra les corrections Δ[Rk]μ. La solution à la μ ième itération sera
contiendra les corrections Δ[Rk]μ. La solution à la μ ième itération sera
puisque la matrice 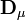 sera carrée et inversible[note 10], [note 11]. Chaque itération nécessitera alors un nouveau calcul de ces dérivés, mais aussi de nouvelles estimations des concentrations, jusqu'à ce que les corrections Δ[Rk] deviennent insignifiantes, et on aura ainsi trouvé les concentrations finales. Le nombre d'itérations requises dépendra du point de départ, c'est-à-dire de la qualité des valeurs estimées des concentrations [R] à la première itération. Dans le cadre d'une titration, où chaque échantillon (suite à chaque ajout du titrant) suit l'autre en ordre, on n'aura besoin d'estimer ces concentrations qu'au début et le nombre d'itérations à chaque échantillon suivant sera réduit[note 12].
sera carrée et inversible[note 10], [note 11]. Chaque itération nécessitera alors un nouveau calcul de ces dérivés, mais aussi de nouvelles estimations des concentrations, jusqu'à ce que les corrections Δ[Rk] deviennent insignifiantes, et on aura ainsi trouvé les concentrations finales. Le nombre d'itérations requises dépendra du point de départ, c'est-à-dire de la qualité des valeurs estimées des concentrations [R] à la première itération. Dans le cadre d'une titration, où chaque échantillon (suite à chaque ajout du titrant) suit l'autre en ordre, on n'aura besoin d'estimer ces concentrations qu'au début et le nombre d'itérations à chaque échantillon suivant sera réduit[note 12].
Affinement des constantes d'équilibre
L'affinement des valeurs des constantes d'équilibre inconnues se fait d'habitude en minimisant, par la méthode des moindres carrés non-linéaire, une quantité U (aussi dénoté par χ2) nommée fonction objectif :
où les y représentent les mesures et les ycalc sont les quantités que les concentrations des espèces permettent d'anticiper. La matrice des pondérations, 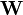 , devrait, à l'idéal, être l'inverse de la matrice des variances et covariances des mesures, mais il est rare que ces quantités soient connaissables à l'avance[note 13]. Si les mesures sont indépendantes l'une de l'autre, les covariances seront nulles et on pourra anticiper les variances relatives, dans lequel cas
, devrait, à l'idéal, être l'inverse de la matrice des variances et covariances des mesures, mais il est rare que ces quantités soient connaissables à l'avance[note 13]. Si les mesures sont indépendantes l'une de l'autre, les covariances seront nulles et on pourra anticiper les variances relatives, dans lequel cas 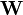 sera une matrice diagonale, et la quantité à minimiser se simplifie ainsi
sera une matrice diagonale, et la quantité à minimiser se simplifie ainsi
où Wi, j = 0 lorsque 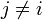 . Des pondérations unitaires, Wi, i = 1, sont fréquemment utilisées[note 14], mais, à moins que les données soient de fiabilité égale, les résultats seront biaisés par les données moins fiables.
. Des pondérations unitaires, Wi, i = 1, sont fréquemment utilisées[note 14], mais, à moins que les données soient de fiabilité égale, les résultats seront biaisés par les données moins fiables.
Les éléments sur la diagonale Wi, i peuvent être estimés par la propagation des erreurs avec
pour l'ensemble des paramètres Q (les variables et constantes connues) qui ne seront pas déterminés mais qui forment des sources d'erreurs expérimentales, où σ (Qj) est une estimation réaliste de l'incertitude sur la valeur du j ième paramètre Q[note 15]. Ceci reconnaît que chaque paramètre n'aura pas obligatoirement une influence uniforme sur l'ensemble des échantillons, et la contribution de chaque résidu (y − ycalc) sera désaccentuée selon son incertitude cumulée de l'ensemble des sources d'erreur.
On peut habituellement trouver le U minimum en mettant à zéro les dérivées de U comparé à chaque paramètre inconnu P, mais on ne peut pas en retirer les valeurs des P directement[note 16]. Plutôt, tout comme au cours du calcul des concentrations (section précédente), la méthode Gauss-Newton exprime les mesures sous forme de séries de Taylor tronquées
ou, en forme matricielle-vectorielle,
ou 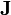 est la matrice des dérivées, nommée matrice jacobienne, et ou le vecteur
est la matrice des dérivées, nommée matrice jacobienne, et ou le vecteur 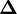 contient les corrections ΔP. Cette fois, on pondère les résidus pour empêcher que le résultat final ne soit biaisé par les erreurs dans les autres paramètres, ainsi
contient les corrections ΔP. Cette fois, on pondère les résidus pour empêcher que le résultat final ne soit biaisé par les erreurs dans les autres paramètres, ainsi
Les corrections ΔP sont calculées avec
où l'exposant T indique la matrice transposée. La matrice 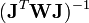 est quelquefois nommée la matrice hessienne (bien que le nom matrice hessienne sert à désigner aussi la matrice des dérivées secondes). Pour fins ultérieurs, nous la représenterons par
est quelquefois nommée la matrice hessienne (bien que le nom matrice hessienne sert à désigner aussi la matrice des dérivées secondes). Pour fins ultérieurs, nous la représenterons par 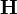 . Les corrections ainsi calculées seront ajoutées aux valeurs des P actuelles pour générer de meilleures estimations pour la prochaine itération. Les concentrations des espèces, les ycalc, les pondérations W et les dérivées dans
. Les corrections ainsi calculées seront ajoutées aux valeurs des P actuelles pour générer de meilleures estimations pour la prochaine itération. Les concentrations des espèces, les ycalc, les pondérations W et les dérivées dans 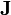 seront tous recalculées pour générer à la prochaine itération une nouvelle série de corrections, et ce de manière répétée jusqu'à ce que les corrections deviennent insignifiantes et que le U soit plus ou moins stabilisé. Alors, on aura déterminé les valeurs finales des P.
seront tous recalculées pour générer à la prochaine itération une nouvelle série de corrections, et ce de manière répétée jusqu'à ce que les corrections deviennent insignifiantes et que le U soit plus ou moins stabilisé. Alors, on aura déterminé les valeurs finales des P.
Modification de Levenberg-Marquardt
Aussi nommée méthode ou algorithme de Marquardt-Levenberg.
Dépendant du point de départ, les corrections de Gauss-Newton peuvent être beaucoup excédentaires, dépassant le minimum, ou menant à une augmentation du U (ce qui causerait normalement un affinement avorté) ou même causer des oscillations autour du minimum. Dans d'autres situations, l'approche du minimum peut être lente. Pour amortir les corrections trop grandes ou accélérer l'atteinte du U minimal, on peut faire appel à l'algorithme de Marquardt-Levenberg, fréquemment utilisée, et appliquer des corrections modifiées
où λ est un paramètre ajustable, et 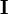 est la matrice identité. Un λ non-zéro oriente la recherche du U minimum vers la direction de la descente de gradient,
est la matrice identité. Un λ non-zéro oriente la recherche du U minimum vers la direction de la descente de gradient, 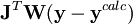 , qui résulte de la minimisation directe de U en mettant à zéro tous ses dérivés comparé aux paramètres P. Cette technique, qui est d'utilité générale pour résoudre les dispositifs d'équations non-linéaires, exige dans le cas des déterminations de constantes d'équilibre un certain nombre de re-calculs itératifs des concentrations pour tester si la valeur actuelle de λ reste utile.
, qui résulte de la minimisation directe de U en mettant à zéro tous ses dérivés comparé aux paramètres P. Cette technique, qui est d'utilité générale pour résoudre les dispositifs d'équations non-linéaires, exige dans le cas des déterminations de constantes d'équilibre un certain nombre de re-calculs itératifs des concentrations pour tester si la valeur actuelle de λ reste utile.
Modification de Potvin
Puisque chaque itération sur les β entraîne un nouveau calcul des concentrations, lui-même itératif, les re-calculs obligations par la technique de Marquardt-Levenberg lors d'une même itération sont coûteux, en particulier s'il y a la plupart de données à traiter. Le même problème survient avec d'autres méthodes d'optimisation numérique à paramètre ajustable, telles que les méthodes de Broyden-Fletcher-Goldfarb-Shanno (recherche linéaire du paramètre optimal) ou de Hartley-Wentworth (recherche parabolique) [7].
Ayant noté que ce sont les corrections positives aux valeurs sous-estimées des log10β (ou négatives aux valeurs sur-estimées des β) qui produisent un dépassement du U minimum, alors que les corrections négatives ne le font pas, et que la taille de ces corrections excessives grandit de façon exponentielle plus on est éloigné du minimum, Potvin (1992a) a proposé une simple modification logarithmique des corrections positives, soit pour la correction Δq du q ième log10β
Cette formulation découle d'une solution approximative des séries de Taylor à ordre illimité. Les corrections ainsi modifiées sont de taille bien plus raisonnable, en particulier si on est loin du minimum. Quoique ces corrections modifiées puissent quand même occasionnellement mener à un léger dépassement du minimum ou même à une augmentation du U, ce ne sera que temporaire puisque l'itération suivante reviendra dans la bonne direction sans dépassement. L'algorithme limite aussi toute correction négative si la descente du gradient propose au contraire une correction positive. Le grand avantage de cette modification est son coût minime.
Particularités pour données spectrophotométriques
Selon le modèle chimique général exposé plus haut, la loi de Beer-Lambert peut être ré-écrite en termes des concentration des espèces E
qui, en notation matricielle, donne
où la matrice 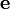 contient les ελ. On peut distinguer les espèces non-chromophores des chromophores avec les valeurs d'ε des espèces non-chromophores obligatoirement zéro et tenues à zéro comme paramètres fixes. Si les valeurs d'ε d'une espèce spécifique (par exemple, une espèce limitative) sont connues, elles pourront aussi être tenues fixes.
contient les ελ. On peut distinguer les espèces non-chromophores des chromophores avec les valeurs d'ε des espèces non-chromophores obligatoirement zéro et tenues à zéro comme paramètres fixes. Si les valeurs d'ε d'une espèce spécifique (par exemple, une espèce limitative) sont connues, elles pourront aussi être tenues fixes.
Il y a deux approches le plus souvent adoptées pour le calcul des constantes d'équilibre et des ε inconnus. On peut ré-exprimer les ε en fonctions des absorbances et écrire
![\mathbf{A}= \{ (\mathbf{[E]}ˆT \mathbf{[E]})ˆ{-1} \mathbf{[E]}ˆT \mathbf{A}\} \mathbf{[E]}](illustrations/6e4e03fbe7649060e0301cdd36b5c576.png) ,
,
ce qui permettra un affinement simultané des constantes d'équilibre et des ε inconnus[note 17]. L'autre approche, celle utilisée par les auteurs de Hyperquad[8] et de Specfit[9] par exemple, consiste à séparer le calcul des ε de celui des constantes d'équilibre, de n'affiner que les constantes d'équilibre et de calculer les ε avec les concentrations résultantes. Ainsi, en partant d'une série de valeurs estimées des ε, on affine les constantes d'équilibre en optimisant l'accord du modèle avec les mesures d'absorbance avec la Jacobienne, comme décrit ci-haut, puis les ε sont mis à jour avec
et les nouvelles concentrations [E] qui en résultent[note 18]. Par la suite, on utilise ces nouvelles estimations des ε pour lancer un nouvel affinement des constantes d'équilibre, ce qui mène à une nouvelle série d'estimations des ε, et ainsi de suite. Ce ping-pong continue jusqu'à ce que les deux familles de paramètres ne changent plus. Les auteurs de Specfit[9] montrent comment trouver les dérivés de la matrice pseudo-inverse ![(\mathbf{[E]}ˆT \mathbf{[E]})ˆ{-1} \mathbf{[E]}ˆT](illustrations/b510e304fad8803001f2d2ec16c4f098.png) .
.
Particularités pour données par RMN
La formulation usuelle, présentée au départ, qui relie la mesure 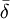 aux fractions molaires des noyaux participants, ci / Σci, ne convient pas ici et peut même induire en erreur[note 19]. Puisque l'ensemble des noyaux contribuant à un signal donné proviennent du même réactif, dont la concentration totale est connue et constante, et puisqu'une même espèce porteuse peut porter plus qu'un de ce réactif, une représentation plus générale qui reprend la notation utilisée ailleurs dans cet article relie un signal provenant du k ième réactif aux concentrations d'espèces avec
aux fractions molaires des noyaux participants, ci / Σci, ne convient pas ici et peut même induire en erreur[note 19]. Puisque l'ensemble des noyaux contribuant à un signal donné proviennent du même réactif, dont la concentration totale est connue et constante, et puisqu'une même espèce porteuse peut porter plus qu'un de ce réactif, une représentation plus générale qui reprend la notation utilisée ailleurs dans cet article relie un signal provenant du k ième réactif aux concentrations d'espèces avec
L'utilisation ici de la concentration analytique [Rk]connue, plutôt que la somme des parts appartenant à chaque espèce, [Rk]calc, renforce le fait que le dénominateur commun à l'ensemble des fractions molaires est constant et ne fluctue pas avec les β[note 20]. Lors du calcul des concentrations à chaque itération sur les β, les [Rk]calc seront de toute façon ajusté de sorte à égaler les [Rk]connue.
En notation matricielle, on a
où la matrice 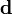 contient les éléments δi. Les auteurs de HypNMR[note 21] procèdent comme pour les données spectrophotométriques, c'est-à-dire que la Jacobienne inclut les dérivés comparé aux β ainsi qu'aux δ, mais que seuls les β sont corrigés tandis que les δ sont mis à jour à partir des nouvelles concentrations résultantes, avec
contient les éléments δi. Les auteurs de HypNMR[note 21] procèdent comme pour les données spectrophotométriques, c'est-à-dire que la Jacobienne inclut les dérivés comparé aux β ainsi qu'aux δ, mais que seuls les β sont corrigés tandis que les δ sont mis à jour à partir des nouvelles concentrations résultantes, avec
Analyse des résultats
Fiabilité de la détermination et affinement du modèle
Une détermination numérique forme un test d'un modèle, et non pas une preuve de sa pertinence. On peut examiner la fiabilité du modèle avec l'accord-type, des incertitudes et des corrélations et songer à modifier le modèle pour une détermination plus fiable. Cependant, la détermination cesse alors d'être une mesure de constantes d'équilibres connus et risque de devenir une découverte d'équilibres[note 22]. Cela doit se faire sagement, en se guidant avec des comparaisons impartiales entre modèles.
L'incertitude dans la valeur du j ième paramètre P est apportée par le j, j ième élément (le j ième sur la diagonale) de la matrice 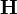 :
:
où σ0 est l'incertitude d'une observation à pondération 1, l'accord-type, qui peut être estimé (selon Alcock et al. , 1978) avec
pour NP paramètres déterminés à partir de ND données expérimentales.
D'un point de vue statistique, l'incertitude dans la valeur d'un paramètre dénote une plage de valeurs, la taille de laquelle dépendra du niveau de confiance qu'on désire, qui générera des modèles indiscernables. Ainsi, les incertitudes reflètent l'incapacité des valeurs des paramètres de reproduire les données. Inversement, les incertitudes reflètent l'incapacité des données expérimentales de préciser les valeurs des paramètres. Certaines modifications à la conception ou à la conduite de l'expérience pourraient plus exactement établir les valeurs des paramètres incertains[note 23]. Autrement, il se peut qu'un paramètre hautement incertain puisse être laissé tomber du modèle chimique sans dégradation'importante'de l'accord du modèle avec les données.
Les cœfficients de corrélation entre les valeurs des paramètres sont rapportés par les éléments hors-diagonale de la matrice 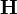 . Entre les valeurs des j ième et k ième paramètres, on calcule
. Entre les valeurs des j ième et k ième paramètres, on calcule
Ceux-ci reflètent l'interdépendance des paramètres en modélisant les données, i. e. l'importance d'inclure chaque paramètre dans le modèle chimique. Inversement, les cœfficients de corrélation reflètent l'incapacité des données à différencier entre les paramètres. Ici encore, certaines modifications expérimentales pourraient y remédier, mais il se peut qu'une paire de paramètres dont les valeurs sont hautement co-reliées puisse être remplacée dans le modèle chimique par un seul paramètre, sans dégradation'importante'de l'accord du modèle avec les données.
D'autre part, il se peut que le modèle chimique donne un accord'insatisfaisant'avec les données, selon la taille du σ0 et celle des résidus, mais il serait utile de savoir ce qui forme un accord'satisfaisant'. Selon Hamilton (1964), si la condition pour ND données
est remplie, l'accord est satisfaisant[note 24]. La quantité σi représente l'incertitude anticipée sur la i ième mesure. Si on suit la pratique prescrite ci-haut, on anticipera les valeurs de ces σi en prédisant à quel degré les erreurs expérimentales (estimées et anticipées) dans les paramètres fixes Q affecteront les mesures prédites (ycalc). Si, aussi, on utilise ces σi dans les pondérations, avec 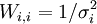 , alors la condition qui indiquera un accord satisfaisant entre yobs et ycalc deviendra
, alors la condition qui indiquera un accord satisfaisant entre yobs et ycalc deviendra
ou, écrit plus simplement, U < ND pour ND données. C'est-à-dire qu'un accord satisfaisant donne des écarts entre mesures (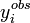 ) et calculs (
) et calculs (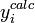 ) qui, globalement sinon à chaque fois, tombent en deça des σi, la marge d'incertitude qu'on s'accordait au départ.
) qui, globalement sinon à chaque fois, tombent en deça des σi, la marge d'incertitude qu'on s'accordait au départ.
Dans le cas d'un accord insatisfaisant, l'inclusion d'autres espèces (et d'autres paramètres β) pourrait l'perfectionner. Dans la mesure où l'ajout d'un paramètre d'habitude perfectionnera l'accord, tandis que l'élimination d'un paramètre d'habitude l'empirera, il devient important de comprendre ce qui forme une dégradation ou amélioration'importante'. Une altération d'un modèle chimique, en particulier l'inclusion d'une espèce inattendue ou la mise de côté d'une espèce attendue, doit être guidée par le bon sens chimique et être impartial. Pour aider une décision impartiale si on expérimente avec divers modèles chimiques, le test de Hamilton[note 25] (Hamilton, 1964) utilisé fréquemment en cristallographie, permet aux données de décider si un modèle alternatif devrait être rejeté ou accepté.
Finalement, les mesures elles-mêmes mais aussi les paramètres Q influenceront la qualité de l'accord. A titre d'exemple, certaines données extrêmes ou aberrantes peuvent être'problématiques'en ce que leur mise à l'écart perfectionne de façon'importante'la qualité de l'accord, et ainsi diminué les incertitudes dans les P, au contraire de la règle générale que l'accord et les incertitudes seront perfectionnés par un plus grand nombre de données. D'autre part, les résidus yobs − ycalc peuvent être co-reliés, c'est-à-dire que les yobs ne sont pas distribués de façon aléatoire de part et d'autre des ycalc, ce que la méthode des moindres carrés supposera[note 26]. Pour remédier à de tels problèmes, on peut omettre certaines données, ou déplacer la pondération en changeant les σ (Q) , ou changer les Q eux-mêmes, ou même les affiner aux côtés des paramètres P comme s'ils devaient être déterminés (ce que certains logiciels permettent). Ce genre de bricolage pour la simple amélioration de l'accord biaise le modèle au risque d'une perte de sens. Le bon sens chimique, plutôt qu'un penchant pour un résultat, devrait guider tout changement au modèle, aux paramètres fixes, aux données ou à leur pondération, et le mal qu'on se donnerait pour perfectionner un accord ou un modèle pourraient être orientés à perfectionner la qualité des données (i. e. la confiance en elles) [note 27].
Cependant, il peut être utile quelquefois de rigoureusement comparer les résultats découlant d'altérations judicieuses au modèle. L'omission ou la désaccentuation de données et l'altération de paramètres fixes donnent lieu à des modèles compétiteurs où les matrices 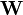 changent, et un test de Hamilton modifié[note 28] peut décider lesquels sont différents de façon statistiquement significative. Ce test modifié est aussi utile pour la comparaison de résultats provenant d'expériences scindées, avec différentes données et différentes matrices
changent, et un test de Hamilton modifié[note 28] peut décider lesquels sont différents de façon statistiquement significative. Ce test modifié est aussi utile pour la comparaison de résultats provenant d'expériences scindées, avec différentes données et différentes matrices 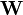 .
.
Erreurs expérimentales
Comme indiqué plus tôt, les incertitudes calculées avec la matrice 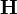 reflètent la qualité du modèle et connotent sa'déterminabilité'. Les valeurs des paramètres et leurs incertitudes seront bien reproduites si l'expérience était répétée sous des conditions semblables, mais la'reproduictibilité'd'une détermination dénote l'attente de résultats statistiquement indiscernables à partir de mesures totalement indépendantes, à l'idéal par différents praticiens avec instruments différents et différentes concentrations des mêmes matériaux de différentes provenances. Le plus fréquemment, une telle diversité de sources de données n'est pas envisageable[note 29]. La répétition d'une même expérience demeure cependant utile pour amoindrir les effets d'erreurs aléatoires dans certaines sources d'erreurs systématiques Q[note 30].
reflètent la qualité du modèle et connotent sa'déterminabilité'. Les valeurs des paramètres et leurs incertitudes seront bien reproduites si l'expérience était répétée sous des conditions semblables, mais la'reproduictibilité'd'une détermination dénote l'attente de résultats statistiquement indiscernables à partir de mesures totalement indépendantes, à l'idéal par différents praticiens avec instruments différents et différentes concentrations des mêmes matériaux de différentes provenances. Le plus fréquemment, une telle diversité de sources de données n'est pas envisageable[note 29]. La répétition d'une même expérience demeure cependant utile pour amoindrir les effets d'erreurs aléatoires dans certaines sources d'erreurs systématiques Q[note 30].
L'estimation de'l'erreur expérimentale'dans une constante d'équilibre peut par conséquent se faire avec une seule valeur de σ provenant d'une seule détermination, ou de plusieurs déterminations répétées pour amoindrir les effets d'erreurs aléatoires dans certaines sources d'erreurs systématiques Q, jusqu'à la combinaison d'expériences totalement indépendantes où les effets de l'ensemble des sources d'erreurs systématiques seront amoindris. Donc, toute estimation'd'erreur expérimentale'devrait aussi communiquer la diversité des données utilisées pour l'estimation. Cependant, la simple prise d'une moyenne des valeurs séparément déterminées ne tiendra pas compte de la fiabilité inégale des déterminations, telle que rapportée par les incertitudes calculées dans chaque détermination. Plutôt, la moyenne 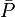 des valeurs individuelles pondérées par leurs incertitudes s'appuiera davantage sur les valeurs les moins incertaines avec
des valeurs individuelles pondérées par leurs incertitudes s'appuiera davantage sur les valeurs les moins incertaines avec
où σn (Pn) rapporte l'incertitude de la n ième de N déterminations d'un même paramètre P. Pourvu que les tailles relatives des pondérations soient justes, cette moyenne sera insensible aux valeurs absolues de ces pondérations. De même, on peut quantifier'l'erreur expérimentale'du 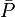 avec l'écart-type
avec l'écart-type 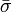 autour de la moyenne, où les écarts
autour de la moyenne, où les écarts 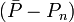 sont pondérés par ces mêmes incertitudes, selon Potvin (1994) :
sont pondérés par ces mêmes incertitudes, selon Potvin (1994) :
Constantes dérivées et modèles équivalents
Si on calcule une constante d'équilibre qui dépend de constantes de formation qu'on a déterminées, telle qu'un Ka, l'incertitude d'une telle constante dérivée n'est pas une simple fonction des incertitudes dans les constantes déterminées, comme le voudraient les règles normales de la propagation d'erreurs, puisque cela requiert que les sources d'erreur soient indépendantes tandis que les constantes déterminées par les mêmes données sont co-reliées. En guise d'exemple, pour la protonation d'une substance dibasique L,
![K_{a1} = \frac {[LHˆ+]}{[Hˆ+][L]} = \beta_{LHˆ{+}}](illustrations/d31bd239ad5acc2fd53f1b6ff75f8e15.png) , ou
, ou 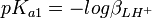 et
et![K_{a2} = \frac {[Hˆ+][LHˆ+]}{[LH_2ˆ{2+}]} = \frac {[Hˆ+]ˆ2[L]}{[LH_2ˆ{2+}]} \frac {[LHˆ+]}{[Hˆ+][L]} = \frac {\beta_{LHˆ{+}}}{\beta_{LH_2ˆ{2+}}}](illustrations/8d2c95fafd00f55a91a3f4daecee42ce.png) , ou
, ou 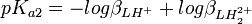
L'incertitude et la variance sur la valeur de pKa1 sont les mêmes que sur 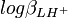 mais la variance (l'incertitude au carré) sur la valeur de pKa2, σ2 (pKa2) , n'est pas obligatoirement la somme des variances sur
mais la variance (l'incertitude au carré) sur la valeur de pKa2, σ2 (pKa2) , n'est pas obligatoirement la somme des variances sur 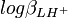 et
et 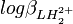 , à cause de la corrélation (d'habitude) non-zéro entre les deux logβ. En réalité,
, à cause de la corrélation (d'habitude) non-zéro entre les deux logβ. En réalité,
où 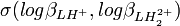 est le cœfficient de corrélation entre
est le cœfficient de corrélation entre 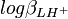 et
et 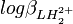 . Les cœfficients de corrélation entre constantes dérivées sont aussi des fonctions de celles entre les constantes de formation. Puisque l'erreur est positive mais que les cœfficients de corrélation peuvent être négatifs, l'incertitude sur la valeur des constantes dérivées peut être soit plus grande ou plus petite que ce que les règles normales de la propagation d'erreur auraient prévues. Parce que les constantes de protonation
. Les cœfficients de corrélation entre constantes dérivées sont aussi des fonctions de celles entre les constantes de formation. Puisque l'erreur est positive mais que les cœfficients de corrélation peuvent être négatifs, l'incertitude sur la valeur des constantes dérivées peut être soit plus grande ou plus petite que ce que les règles normales de la propagation d'erreur auraient prévues. Parce que les constantes de protonation 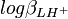 et
et 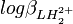 sont certainement co-reliées négativement (un agrandissement de l'une entraînerait un amoindrissement compensatoire de l'autre pour rétablir un accord aux données), l'incertitude sur pKa2 sera certainement plus grande que celle anticipée par la propagation d'erreur normale.
sont certainement co-reliées négativement (un agrandissement de l'une entraînerait un amoindrissement compensatoire de l'autre pour rétablir un accord aux données), l'incertitude sur pKa2 sera certainement plus grande que celle anticipée par la propagation d'erreur normale.
Les constantes dérivées forment une représentation équivalente d'un modèle chimique. Dans cet exemple, pKa1 et pKa2 peuvent entièrement et de façon entièrement équivalente remplacer 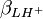 et
et 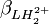 , même si l'une ou l'autre de ces représentations est employée dans l'affinement du modèle parce qu'exigé par le logiciel ou par choix personnel, mais les rapports d'erreurs entre les paramètres (variance et covariance) fluctueront d'une représentation à l'autre, comme l'exemple ici le démontre.
, même si l'une ou l'autre de ces représentations est employée dans l'affinement du modèle parce qu'exigé par le logiciel ou par choix personnel, mais les rapports d'erreurs entre les paramètres (variance et covariance) fluctueront d'une représentation à l'autre, comme l'exemple ici le démontre.
Quelquefois même, un modèle construit d'équilibres de formation (avec constantes β) n'est pas le mieux adapté au dispositif expérimental. Tout équilibre de formation présume que les concentrations des réactifs libres ne seront pas négligeables tandis que, dans bien des cas, les constantes de formation sont tellement grandes qu'il ne reste presque plus de l'un ou d'un autre réactif en forme libre. Cela peut donner des difficultés pendant les calculs des concentrations, des valeurs de β particulièrement incertaines et un calcul de constantes dérivées qui met en œuvre des constantes β particulièrement incertaines[note 31].
Potvin (1990b) a présenté une manière de construire des modèles équivalents, d'en déduire les rapports d'erreur et d'éviter de devoir composer avec des concentrations négligeables en réactifs libres.
Logiciels
La plupart de logiciels visant le calcul de constantes d'équilibre est paru dans la littérature scientifique, pas tous aussi utiles ou rigoureux[10].
Les logiciels les plus utilisés sont :
- données potentiométriques ou pH-métriques : Hyperquad[8], BEST (Martell et Motekaitis, 1992), PSEQUAD[11]
- données spectrophotométriques : Hyperquad, SQUAD[11], Specfit[9] (Specfit/32 est un produit commercial)
- données de RMN : HypNMR[12], [13]
On peut habituellement faire les calculs nécessaires de manière dynamique avec logiciels à feuilles de calcul. Pour certains dispositifs simples, il existe des feuilles de calcul pré-conçues pour ce faire[14] mais leurs calculs ne suivent pas le cheminement exposé ici et utilisent le module boîte-noire SOLVER[15] pour réaliser les minimisations par la méthode des moindres carrés.
Particularités
Certains logiciels ont été écrits pour des ordinateurs depuis longtemps obsolètes. Quelquefois, ils auront été modernisés dans des mises en œuvre locales.
La plupart des logiciels suivent la méthode Gauss-Newton décrite ici. En réalité, l'approche numérique importe peu, pourvu que le minimum de la fonction objectif soit bel et bien atteint, puisque le même minimum devrait être atteint par l'ensemble des approches à partir des mêmes données. Cependant, le minimum à atteindre et , par conséquent, les résultats ultimes dépendent de la pondération utilisée, et les logiciels sont inégaux sur cet aspect. Aussi, le calcul correct des incertitudes sur les paramètres requiert la Jacobienne (complète si on traite plus d'une sorte de données), mais dépend aussi de la pondération utilisée. Sur ces aspects, certaines particularités de ces logiciels sont à noter :
- BEST est conçu pour les titrations pH-métriques et utilise une pondération selon la pente locale de la courbe pH-volume. La recherche du minimum se fait heuristiquement, ce qui évite le calcul de dérivées mais qui nécessite énormément d'itérations, et peut être erroné. Aucune estimation des incertitudes n'est envisageable.
- Hyperquad peut traiter des données potentiométriques et spectrophotométriques en même temps, ce qui nécessite qu'on minimise une double somme des carrés, pratique douteuse qui mène à des résultats biaisés. Ceci nécessite aussi une jacobienne qui comprend des éléments mixtes aux tailles envisageablement dissemblables, ce qui peut rendre la recherche du minimum problématique. C'est peut-être la raison pour laquelle ce logiciel utilise l'algorithme de Levenberg-Marquardt. Même si uniquement une sorte de données est traitée, la pondération ne prend en compte que les erreurs probables en volume de titrant et en mesure, ce qui biaise aussi les résultats et les incertitudes. HypNMR, des mêmes auteurs, semble suivre cet exemple.
- Specfit utilise l'analyse en composantes principales[note 32] pour choisir les longueurs d'onde les plus déterminantes auxquelles modeler l'absorbance. Ce logiciel semble n'utiliser aucune pondération des données.
- HypNMR semble aussi ne prendre en compte que les erreurs probables en volume de titrant et en mesure pour pondérer, tout comme Hyperquad par les mêmes auteurs, ce qui biaise aussi les résultats et les incertitudes.
- EQNMR normalement n'utilise pas de pondération, et le détail du calcul des incertitudes n'est pas clarifié et provient apparemment d'un rapport technique et d'une publication inaccessibles. L'algorithme de l'affinement est décrit en termes généraux dans une publication de 1968[16] et une autre de 1973[17] qui, elles aussi, font référence à des rapports techniques inaccessibles.
Annexes
Notes
- En RMN dynamique (en) , un équilibre suffisamment lent pour faire voir deux signaux doit procéder avec une constante de vitesse tombant sous le seuil de la coalescence des pics donné par
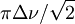 , où Δν est la différence des fréquences des signaux provenant de chaque espèce en équilibre, correspondant à
, où Δν est la différence des fréquences des signaux provenant de chaque espèce en équilibre, correspondant à 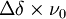 où ν0 est la fréquence opérationnelle du spectromètre et Δδ est la différence des déplacements chimiques des deux signaux. Une intégration précise des deux signaux nécessite une séparation entre eux supérieure à la largeur-type d'un signal, ce qui sera facilité par une constante de vitesse largement inférieure à ce seuil. Une constante de vitesse supérieure à ce seuil donnera un seul signal.
où ν0 est la fréquence opérationnelle du spectromètre et Δδ est la différence des déplacements chimiques des deux signaux. Une intégration précise des deux signaux nécessite une séparation entre eux supérieure à la largeur-type d'un signal, ce qui sera facilité par une constante de vitesse largement inférieure à ce seuil. Une constante de vitesse supérieure à ce seuil donnera un seul signal. - Surtout, il faut un délai suffisamment long entre pulsions pour assurer une relaxation quasi-totale des noyaux, une ligne de base aplanie et un déphasage quasi-nul de part et d'autre des signaux.
- Cette formulation habituelle suffit pour les dispositifs d'équilibre simples, mais peut porter à confusion dans une formulation qui se veut générale, telle qu'exposée dans une section ultérieure. On devra distinguer la concentration c d'un noyau contribuant à un signal donné de la concentration [E] de l'espèce porteuse du noyau, puisqu'une espèce peut porter plus d'un même noyau, et distinguer aussi par conséquent la somme des concentrations de ce noyau de la somme des concentrations des espèces.
- Un modèle linéaire exige aussi que les variables (les x dans y = mx + b) soient sans erreur. Ceci est quasiment impossible en science, car il y aura presque toujours une erreur dans toute quantité mesurable. Cependant, York (D. York, Can. J. Phys. 44 (1966) 1079) a démontré que de petites erreurs dans les variables auront un effet négligeable sur la solution finale du rapport linéaire. Qui plus est , Berkson (J. Berkson, J. Am. Stat. Soc. 45 (1950) 164) a démontré que ces erreurs sont acceptables si les valeurs des x sont visées ou précisées (par exemple en livrant un volume précis décidé à l'avance) et non pas aléatoire (comme ce sera le cas, par exemple, si on cherchait la relation entre chiffre d'affaires et nombres de clients, où le nombre de clients de jour en jour est aléatoire), pourvu que ces erreurs sont indépendantes des variables et des mesures. Cette indépendance n'est cependant pas assurée. A titre d'exemple, si la variable x est un volume livré par burette mal calibrée, les erreurs dans les x seront systématiques et non pas aléatoires.
- C'est précisément ce qu'on demande des étudiants en travaux pratiques de l'université américaine.
- Tout comme dans les dispositifs d'équations linéaires, il faut tout autant d'équations indépendantes qu'il y a de paramètres indépendants à déterminer. Avec un ensemble d'équilibres à constantes données, on trouvera la solution unique de la totalité des concentrations des espèces. Plus tard, avec une mesure de la concentration d'une espèce, on trouvera la solution unique de la totalité des constantes d'équilibre. Il faut par conséquent au minimum tout autant de quantités connues qu'il y aura d'inconnues pour obtenir une solution unique. On peut toujours définir un plus grand nombre d'équilibres que d'espèces, mais certains seront redondants parce qu'ils ne seront pas indépendants, c'est-à-dire qu'ils seront une combinaison quelconque des autres équilibres déjà définis; on ne pourra pas déterminer l'un indépendamment de l'autre et on ne doit par conséquent pas les définir comme s'ils étaient indépendants.
- À la section Constantes dérivées et modèles équivalents, on verra comment certains dispositifs d'équilibres seront mieux modelés autrement.
- L'expérience montre qu'il n'y a pas d'avantage à y inclure des termes d'ordre supérieur, puisque l'accélération à la solution que cela peut donner, par une réduction du nombre d'itérations requises, est insuffisante pour justifier les calculs plus compliqués que cela nécessite à chaque itération (et la programmation de ces calculs plus compliquée).
-
![{\partial [R_j]_{\mu}ˆ{calc}}/{\partial [R_k]} = \sum_iˆ{N_E} a_{i,j}[E_i]_{\mu}a_{i,k}/[R_k]_{\mu}](illustrations/b3d1780a18ecac179d0b7e66e6f34246.png)
- Motekaitis et Martell (1982) arrivent au même résultat avec des déterminantes.
- Ceci illustre le grand avantage de la représentation par équilibres de formation cumulative : n'importe quel nombre d'espèces en solution sont définies en termes d'un nombre bien plus petit de réactifs, ce qui nécessite la solution d'un ensemble plus petit d'équations simultanées, l'inversion d'une matrice plus petite, et par conséquent un calcul plus rapide. À cet égard, cette approche numérique diverge de celle d'Alcock et al. (1978), qui ont cherché les concentrations de l'ensemble des espèces à la fois.
- Les valeurs finales des concentrations calculées pour un échantillon peuvent servir comme estimations au début du calcul pour l'échantillon suivant. Les dérivés qu'on aura calculés à la dernière itération de l'une serviront à la première itération de l'autre, la matrice
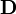 correspondante aura déjà été invertie, et on aura aussitôt un premier ensemble de corrections Δ[Rk] à apporter. Ainsi, quelques itérations suffiront le plus souvent pour chaque échantillon, sauf aux points d'inflexion, où les concentrations changent plus radicalement.
correspondante aura déjà été invertie, et on aura aussitôt un premier ensemble de corrections Δ[Rk] à apporter. Ainsi, quelques itérations suffiront le plus souvent pour chaque échantillon, sauf aux points d'inflexion, où les concentrations changent plus radicalement. - Lorsqu'elle s le sont , la valeur anticipée du U est 1, ce qui veut dire que les mesures auront été reproduites en deçà des erreurs expérimentales.
- Dans ce cas, la valeur anticipée du U est la des erreurs expérimentales.
- On présume ici que ces sources d'erreurs sont indépendantes, ce qui est le plus fréquemment le cas, sinon on devra estimer leurs covariances σ (Qj, Qk) et ajouter au calcul des
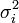 les contributions appropriées, soit
les contributions appropriées, soit 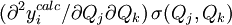 .
. - Ceci générera les équations simultanées
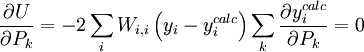 ,
,
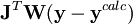 , où la matrice
, où la matrice 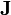 , nommée matrice jacobienne, contiendra comme éléments les dérivés
, nommée matrice jacobienne, contiendra comme éléments les dérivés 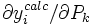 . La méthode de la descente de gradient présume qu'à l'approche du minimum, les corrections à apporter aux P pour en arriver aux valeurs finales
. La méthode de la descente de gradient présume qu'à l'approche du minimum, les corrections à apporter aux P pour en arriver aux valeurs finales 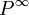 seront approximativement
seront approximativement
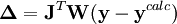 . Cependant, cette méthode est inefficace car elle nécessite une pondération (une optimisation) des corrections, soit parce qu'elles sont trop grandes loin du minimum ou trop petites proche du minimum, ce qui requiert des re-calculs lors d'une même itération.
. Cependant, cette méthode est inefficace car elle nécessite une pondération (une optimisation) des corrections, soit parce qu'elles sont trop grandes loin du minimum ou trop petites proche du minimum, ce qui requiert des re-calculs lors d'une même itération. - Mis à part le traitement mathématique spécial que cela exige, il se peut particulièrement quoiqu'à un stage intermédiaire de l'affinement, les corrections aux constantes d'équilibre'divergent'de celles aux ε, c'est-à-dire qu'une série de corrections produit une augmentation des absorbances calculées (ycalc) tandis que l'autre tente de les diminuer, pour ainsi ralentir ou stopper le progrès.
- Cette ruse affine les concentrations (par l'entremise des constantes d'équilibre) tout en proférant de nouvelles estimations plus concordantes des valeurs des ε. C'est une approche qui assure que les deux genres de paramètres seront toujours de mèche et ne divergeront jamais. Même si les ε ne sont pas corrigés en même temps que les constantes d'équilibre, la Jacobienne utilisée comprend les dérivés comparé aux ε pour quand même informer le calcul des corrections aux constantes d'équilibre. Cette utilisation de la Jacobienne complète évite de biaiser l'accord du modèle et de tomber dans un minimum local dû à l'optimisation d'un seul genre de paramètre. En plus, elle permet un calcul ultime des incertitudes sur les ε déterminés.
- L'expression semble non-linéaire en c, et on serait mené à construire la Jacobienne avec des dérivés à deux termes, c'est-à-dire
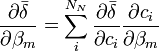
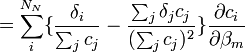
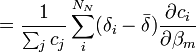
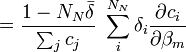 ,
,
- Ceci donne le dérivé plus simple et plus correct
![\frac {\partial \bar{\delta}}{\partial \beta_m} = \frac {1}{[R_k]ˆ{connue}} \sum_iˆ{N_E} \delta_i a_{i,k} \frac {\partial [E_i]}{\partial \beta_m}](illustrations/756fd5a044df4a18ee24dea9ec193489.png) .
.
- Ce que fait le logiciel EQNMR (voir la section Logiciels) n'est pas clair.
- L'obtention d'un meilleur accord avec les données en incluant une espèce, en particulier une inattendue, ne forme pas une preuve absolue de l'existence de cette espèce. Plusieurs revues scientifiques requièrent des preuves indépendantes de nouvelles espèces pour soutenir le modèle chimique. A titre d'exemple, la description de la revue Polyhedron précise que "tout manuscrit ne rapportant que des constantes de stabilité obtenues par titration potentiométrique sans preuve supplémentaire (e. g. spectroscopique) ne sera acceptable" (traduction de l'auteur) (. Consulté le 2007-12-23).
- Les profils des concentrations des espèces ou les'sensibilités'des données (rapportées par les éléments de la matrice jacobienne,
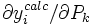 ) pourraient indiquer quelles données s'appuient le plus sur la valeur d'un paramètre spécifique, et ainsi suggérer des modifications envisageables à l'expérience (étendre la plage des données ou ajouter des données interpolantes) or de nouvelles expériences (par exemple, à d'autres concentrations relatives des réactifs) pour accroître la concentration d'une espèce gouvernée par le paramètre.
) pourraient indiquer quelles données s'appuient le plus sur la valeur d'un paramètre spécifique, et ainsi suggérer des modifications envisageables à l'expérience (étendre la plage des données ou ajouter des données interpolantes) or de nouvelles expériences (par exemple, à d'autres concentrations relatives des réactifs) pour accroître la concentration d'une espèce gouvernée par le paramètre. - Cette expression est dérivée de la condition R < Rlim de Hamilton et de ses définitions des facteurs R et Rlim.
- En anglais, "Hamilton R-ratio test".
- Les résidus co-reliés sont particulièrement aisément décelés avec les titrations, et le degré de leur corrélation peut être mesuré. Potvin (1994) donne une formule pour les données de titration dérivée de Neter et al. ( (en) J. Neter, Applied Linear Regression Models, R. D. Irwin, Homewood, IL, 1983). Les résidus hautement co-reliés signalent d'habitude une erreur systématique dans l'un ou l'autre des paramètres fixes du modèle (Q) (volumes, concentrations des réactifs). Aussi, certains logiciels permettent l'inclusion d'impuretés au carbonate contenues dans les réactifs alkalins (venant du CO2 atmosphérique), quoique les tracés de Gran peuvent les quantifier (Martell and Motekaitis, 1992). Finalement, la précipitation soupçonnée mais non détectée d'hydroxydes de métaux de transition, que certains logiciels peuvent anticiper, peut justifier l'exclusion de données au-dessus d'un certain seuil de pH sur la base des valeurs connues de produits de solubilité.
- En guise d'exemple d'un changement justifiable aux paramètres fixes, Martell and Motekaitis (1992) décrivent une situation où un mauvais accord a mené à l'identification d'une impureté dans un réactif, qui pouvait ensuite être corrigée.
- Le test de Hamilton (Hamilton, 1964) compare deux modèles obtenus avec application de la même pondération, i. e. la même matrice
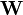 , aux mêmes données. Si on compare deux modèles résultant d'une pondération différente, d'expériences différentes, de différents groupes de données, ou de différentes valeurs des paramètres fixes Q, et par conséquent résultant d'une matrice
, aux mêmes données. Si on compare deux modèles résultant d'une pondération différente, d'expériences différentes, de différents groupes de données, ou de différentes valeurs des paramètres fixes Q, et par conséquent résultant d'une matrice 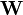 différente, un test qui égalise l'effet de la pondération est parfois utilisé (Potvin, 1994).
différente, un test qui égalise l'effet de la pondération est parfois utilisé (Potvin, 1994). - Même quand des données de sources diverses sont disponibles, elles ne sont pas obligatoirement toutes utiles. En 1982, Braibanti et al. ont analysé la pratique de sept laboratoires et leur variance en déterminant les mêmes équilibres chimiques (A. Braibanti, «Analysis of variance applied to determinations of equilibrium constants», dans Talanta, 1982, p. 725–731), et a rejeté trois des sept séries de résultats pour arriver à des moyennes'globales'.
- À moins d'utiliser un équipement mal réglé, les erreurs aléatoires d'échantillonnage et de mesure s'amoindriront par annulation. Si la préparation d'un échantillon implique le mélange de certains volumes des mêmes solutions, les répétitions réduiront l'effet d'erreurs aléatoires dans ces volumes, mais pas dans les concentrations des solutions. L'utilisation de solutions fraîchement préparées réduira l'effet d'erreurs aléatoires dans leurs préparations (en masses de substance et volumes de solvant), mais pas dans leurs compositions, à moins d'utiliser des lots différents de la même substance. Potvin (1994) a décrit une méthode de calcul de constantes d'équilibre à partir d'expériences de titration qui diminué l'effet d'erreurs aléatoires dans les sources d'erreurs systématiques, au-delà des effets de pondération et de répétition d'expériences.
- Si la concentration d'un réactif en état libre est particulièrement petite dans l'ensemble des échantillons (ou à l'ensemble des points d'une titration) à cause de très grandes constantes pour la formation des espèces complexes l'incorporant, le calcul des concentrations des espèces peut devenir numériquement problématique à cause du besoin d'invertir une matrice
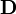 qui contiendra de très petits éléments. Le degré de difficulté dépendra de plusieurs facteurs : la précision des calculs à virgule flottante, les tailles des constantes de formation, les estimations de départ des concentrations à la première itération et des estimations de départ des valeurs des constantes de formation inconnues. L'affinement de constantes β inconnues qui dépendent de très petites concentrations de réactifs peut produire des valeurs hautement incertaines, puisque toute perturbation de la concentration déjà particulièrement petite d'un réactif libre sera particulièrement peu sentie dans les observables calculés (ycalc). A titre d'exemple, une incertitude dans les mesures de pH de ±0.0005 se traduit par une incertitude d'environ ±10-10 M en H+ à pH 7 ou d'environ ±10-5 M à pH 2, et par conséquent une concentration d'un ion métallique tombant sous ces incertitudes ne perturbera pas une compétition entre métal et proton pour un même ligand qu'en deçà de l'erreur de la mesure, et sera par conséquent principalement indécelable et sans conséquence pour le pH calculé. De tels situations peuvent survenir par exemple en présence de complexes ligand-métal particulièrement fortement liés, où il y n'aura jamais des quantités appréciables de métal libre. Finalement, une constante dérivée, telle que celle régissant un échange de ligands, pourrait être d'un plus grand intérêt que les constantes de formation, mais le calcul de constantes dérivées souffrira si elle met en œuvre de très grandes constantes hautement incertaines. Dans de tels situations, on peut reformuler le modèle pour ne jamais impliquer des réactifs libres à concentrations négligeables, ni de constantes de formation impliquant de tels réactifs libres, mais donnant la possibilité de le calcul direct et moins incertain des constantes dérivées.
qui contiendra de très petits éléments. Le degré de difficulté dépendra de plusieurs facteurs : la précision des calculs à virgule flottante, les tailles des constantes de formation, les estimations de départ des concentrations à la première itération et des estimations de départ des valeurs des constantes de formation inconnues. L'affinement de constantes β inconnues qui dépendent de très petites concentrations de réactifs peut produire des valeurs hautement incertaines, puisque toute perturbation de la concentration déjà particulièrement petite d'un réactif libre sera particulièrement peu sentie dans les observables calculés (ycalc). A titre d'exemple, une incertitude dans les mesures de pH de ±0.0005 se traduit par une incertitude d'environ ±10-10 M en H+ à pH 7 ou d'environ ±10-5 M à pH 2, et par conséquent une concentration d'un ion métallique tombant sous ces incertitudes ne perturbera pas une compétition entre métal et proton pour un même ligand qu'en deçà de l'erreur de la mesure, et sera par conséquent principalement indécelable et sans conséquence pour le pH calculé. De tels situations peuvent survenir par exemple en présence de complexes ligand-métal particulièrement fortement liés, où il y n'aura jamais des quantités appréciables de métal libre. Finalement, une constante dérivée, telle que celle régissant un échange de ligands, pourrait être d'un plus grand intérêt que les constantes de formation, mais le calcul de constantes dérivées souffrira si elle met en œuvre de très grandes constantes hautement incertaines. Dans de tels situations, on peut reformuler le modèle pour ne jamais impliquer des réactifs libres à concentrations négligeables, ni de constantes de formation impliquant de tels réactifs libres, mais donnant la possibilité de le calcul direct et moins incertain des constantes dérivées. - En anglais : principal component analysis.
Références
- (en) F. J. C. Rossotti, The determination of stability constants, McGraw-Hill, 1961
- CRC Handbook of Ion Selective Electrodes, CRC Press, Boca Raton, FL, USA.
- A. K. Covington, «Definition of pH Scales, Standard Reference Values, Measurement of pH and Related Terminology», dans Pure Appl. Chem. , 1985, p. 531–542
- Neter et al. (1983) discutent ce sujet en profondeur.
- Spectrophotometric Determination of the pKa of Neutral Red Indicator. Consulté le 2007-12-28
- Pour une compilation des valeurs du KW et de bien d'autres constantes d'équilibre, voir A. E. Martell et R. M. Smith, Critical Stability Constants, Vol. 1-6; Plenum Press : Londres, New York, 1974-1989. Une version électronique version électronique de cette compilation est aussi disponible. Le logiciel MAXC les emploie. Une autre base de données est incorporée dans le logiciel SC-Database ; elle inclut les constantes de solubilité et peut apporter des corrections pour les changements de température et de force ionique. Le site de D. Evans affiche les valeurs de pKa pour plusieurs types d'acides organiques et inorganiques. Avec ces compilations, la valeur d'une constante inconnue peut être estimée à base de valeurs connues de constantes d'équilibres identiques pour bien lancer son affinement.
- Hartley, H. O. Technometrics (1961), 3, 269; Wentworth, W. E. ; W. W. Hirsch; E. Chen. J. Phys. Chem. (1967), 71, 218.
- Hyperquad
- H. Gampp, M. Mæder, C. J. Mayer et A. Zuberbühler, Talanta (1985), 32, 95-101, 257-264.
- Gans, Sabatini et Vacca (1996) en font un survol et donnent une compilation, tout en vantant leur logiciel.
- Computational methods for the determination of formation constants ; D. J. Leggett (éditeur) ; Plenum Press, 1985.
- HypNMR
- EQNMR
- E. J. Billo, EXCEL for Chemists, 2ième éd. ; Wiley-VCH, 2001
- SOLVER
- Fletcher, J. E. ; Spector, A. A. "A procedure for computer analysis of data from macromolecule-ligand binding studies", Comp. Biomed. Res. (1968) 2, 164-175.
- Fletcher, J. E. ; Ashbrook, J. D. ; Spector A. A. "Computer Analysis of Drug-Protein Data" (1973), Ann. New York Acad. Sci. (1973) 226, 69–81.
Bibliographie
- (en) Cet article est partiellement ou en totalité issu de l'article de Wikipédia en anglais intitulé «Determination of equilibrium constants» (voir la liste des auteurs)
- Alcock, R. M., F. R. Hartley et D. E. Rogers (1978) : A Damped Non-linear Least-squares Computer Program (DALSFEK) for the Evaluation of Equilibrium Constants from Spectrophotometric and Potentiometric Data, J. Chem. Soc. Dalton Trans. , 115–123.
- Gans, P., A. Sabatini et A. Vacca (1996) : Investigation of Equilibria in Solution. Determination of equilibrium constants with the Hyperquad suite of programs. Talanta, 43, 1739–1753.
- (en) W. C. Hamilton, Statistics in Physical Science, Ronald Press, New York, 1964
- (en) A. E. Martell, The determination and use of stability constants, Wiley-VCH, 1992
- Motekaitis, R. J. et A. E. Martell (1982) : BEST - a new program for rigourous calculation of equilibrium parameters of complex multicomponent systems, Can. J. Chem. , 60, 2403–2409.
- (en) J. Neter, Applied Linear Regression Models, R. D. Irwin : Homewood, IL, 1983
- Potvin, P. G. (1990a) : Modelling complex solution equilibria. I. Fast, worry-free least-squares refinement of equilibrium constants, Can. J. Chem. , 68, 2198–2207.
- Potvin, P. G. (1990b) : Modelling complex solution equilibria. II. Systems involving ligand substitutions and uncertainties in equilibrium constants derived from formation constants, Can. J. Chem. , 68, 2208–2211.
- Potvin, P. G. (1994) : Modelling complex solution equilibria. III. Error-robust calculation of equilibrium constants from pH or potentiometric titration data, Anal. Chim. Acta, 299, 43–57.
Recherche sur Google Images : |
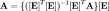
"des constantes d'équilibre" L'image ci-contre est extraite du site fr.wikipedia.org Il est possible que cette image soit réduite par rapport à l'originale. Elle est peut-être protégée par des droits d'auteur. Voir l'image en taille réelle (236 × 24 - 1 ko - png)Refaire la recherche sur Google Images |
Recherche sur Amazone (livres) : |
Voir la liste des contributeurs.
La version présentée ici à été extraite depuis cette source le 30/11/2010.
Ce texte est disponible sous les termes de la licence de documentation libre GNU (GFDL).
La liste des définitions proposées en tête de page est une sélection parmi les résultats obtenus à l'aide de la commande "define:" de Google.
Cette page fait partie du projet Wikibis.

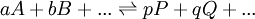
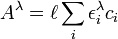
![pH_i = pK_aˆ{HA}+\log_{10} \frac {[Aˆ-]_i}{[HA]_i} = pK_aˆ{HA}+\log_{10} \frac {[OHˆ-]_i}{[HA]_0-[OHˆ-]_i} = pK_aˆ{HA}+\log_{10} \frac {v_i[OHˆ-]_0}{[HA]_0-v_i[OHˆ-]_0}](illustrations/ddb59716dcae281cc790396cce042859.png)
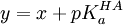
![\log_{10} \frac {[I]_i}{[HIˆ+]_i} = \log_{10} \frac {A_iˆ{\lambda}-\epsilon_{HIˆ+}ˆ{\lambda}\ell[I]_0}{\epsilon_{I}ˆ{\lambda}\ell[I]_0-A_iˆ{\lambda}} = pH_i + pK_aˆ{HI}](illustrations/0629d01c8590789f0b03e45a180adfd1.png)
![\log_{10} \frac {A_iˆ{\lambda}-\epsilon_{HIˆ+}ˆ{\lambda}\ell[I]_0}{\epsilon_{I}ˆ{\lambda}\ell[I]_0-A_iˆ{\lambda}} = pK_aˆ{HA}+\log_{10} \frac {v_i[OHˆ-]_0}{[HA]_0-v_i[OHˆ-]_0}+ pK_aˆ{HI}](illustrations/c19a69dda0e5aa1a67037563c0e326dd.png)
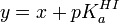
![A_iˆ{\lambda} = f (v_i, [OHˆ-]_0, [A]_0, pK_aˆ{HA}, \epsilon_{I}ˆ{\lambda}, \epsilon_{HIˆ+}ˆ{\lambda}, \ell, [I]_0, pK_aˆI)](illustrations/95cad046c843712a1cab08236a8564df.png)
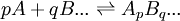
![\beta_{pq...}=\frac{[A_pB_q...]} {[A]ˆp[B]ˆq...}](illustrations/381e4534957fede5aba2929df1f7ecf8.png)
![[E_i] = \beta_i \prod_kˆ{N_R} [R_k]ˆ{a_{i,k}}](illustrations/f96e510fc07e7a9690ff9985ad129f6c.png)
![K_W=[Hˆ+_{ }][OHˆ-]](illustrations/87500672d366e06d4a0aa964bdf0a994.png)
![[R_j]ˆ{calc}= \sum_iˆ{N_E} a_{i,j} [E_i] = \sum_iˆ{N_E} a_{i,j} \beta_{i} \prod_kˆ{N_R} [R_k]ˆ{a_{i,k}}](illustrations/da183564d40dedb2c1c7b720ade499d2.png)
![[R_j]ˆ{connue} = [R_j]_{\mu}ˆ{calc} + \sum_kˆ{N_R} \frac {\partial [R_j]_{\mu}ˆ{calc}}{\partial [R_k]} \Delta [R_k]_{\mu}](illustrations/3a8918672f409e657cd15ee2267ccaa8.png)
![\mathbf{[R]}ˆ{connue} = \mathbf{[R]}_{\mu}ˆ{calc} + \mathbf{D}_{\mu}\, \mathbf{\Delta}_{\mu}](illustrations/8dce58b7a7ba09fa8b3c93676d7df4fe.png)
![\mathbf{\Delta}_{\mu} = \mathbf{D}_{\mu}ˆ{-1}\ (\mathbf{[R]}ˆ{connue} - \mathbf{[R]}_{\mu}ˆ{calc})](illustrations/d40c31ef70568accd464876b3761d8ad.png)
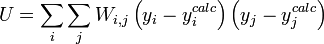
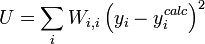
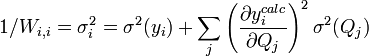
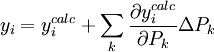
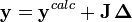
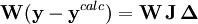
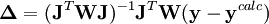
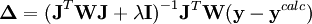
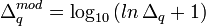
![Aˆ{\lambda}=\ell \sum_i {\epsilonˆ{\lambda}_i [E_i]}](illustrations/37bc164eaa6d9848b0ae6ed4b71701c2.png)
![\mathbf{A}=\ell \, \mathbf{e} \,\mathbf{[E]}](illustrations/ee2afc7e4e8bde9de0b30068e2a79eec.png)
![\mathbf{e} = \{(\mathbf{[E]}ˆT \mathbf{[E]})ˆ{-1} \mathbf{[E]}ˆT \mathbf{A}\} / \ell](illustrations/de3f544869350214ae332cd21110237c.png)
![\bar{\delta} = \frac {1}{[R_k]ˆ{connue}} \sum_iˆ{N_E} \delta_i a_{i,k} [E_i]](illustrations/2c5d516413d020370fdecaeadf983d64.png)
![\mathbf{[R]}ˆ{connue} \mathbf{\bar{\delta}} = \mathbf{a [E] d}](illustrations/5f3331ba06db73c93a0b302cfd5138f3.png)
![\mathbf{d} = [(\mathbf{a [E]})ˆT (\mathbf{a [E]})]ˆ{-1} (\mathbf{a [E]})ˆT \mathbf{[R]}ˆ{connue} \mathbf{\bar{\delta}}](illustrations/cb39285c066c129ae96daecf8348be37.png)
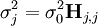
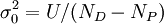
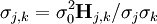
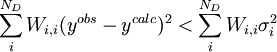
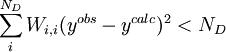
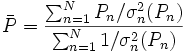
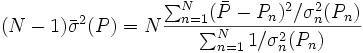
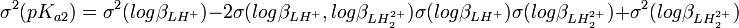
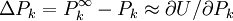

 Accueil
Accueil Recherche
Recherche Début page
Début page Contact
Contact Imprimer
Imprimer Accessibilité
Accessibilité